Обществознание
2023
Какое множество точек задаёт на координатной плоскости неравенство:
a) \((x - 1)(y - 1) \geq 0\);
б) \(x^{2} - y^{2} > 0\)?
а
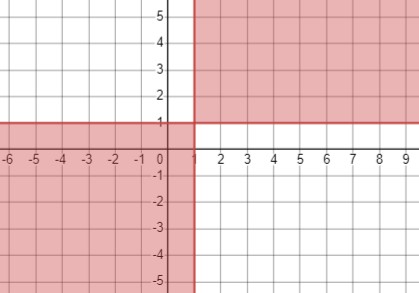
Неравенство \((x-1)(y-1) \geq 0\) можно рассматривать в двух случаях:
\(\left\{\begin{array}{l}x-1 \geq 0 \\ y-1 \geq 0\end{array}\right.\) или \(\left\{\begin{array}{l}x-1 \leq 0 \\ y-1 \leq 0\end{array}\right.\)
Для первого случая получаем \(\left\{\begin{array}{l}x \geq 1 \\ y \geq 1\end{array}\right.\), а для второго \(\left\{\begin{array}{l}x \leq 1 \\ y \leq 1\end{array}\right.\). Таким образом, две области, удовлетворяющие неравенству, находятся между прямыми \(x=1\) и \(y=1\) в первой и третьей координатных четвертях, включая прямые.
б
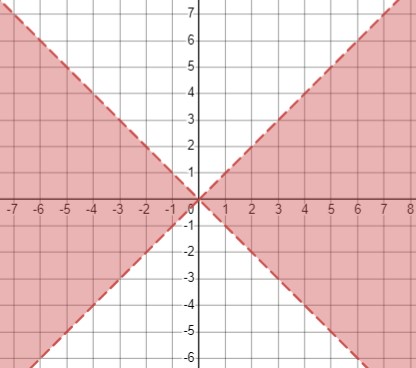
Неравенство \(x^2-y^2>0\) можно представить в виде \((x-y)(x+y)>0\). Рассматривая два случая:
\(\left\{\begin{array}{c}y<x \\ y>-x\end{array}\right.\) или \(\left\{\begin{array}{c}y>x \\ y<-x\end{array}\right.\).
Таким образом, две области, удовлетворяющие неравенству, находятся между прямыми \(y=x\) и \(y=-x\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Какое множество точек задаёт на координатной плоскости неравенство: a) \((x - 1)(y - 1) \geq 0\); б) \(x^{2} - y^{2} > 0\)?
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
