§8. Неравенства с двумя переменными и их системы — Дополнительные упражнения к параграфу 8 — 521 — стр. 148

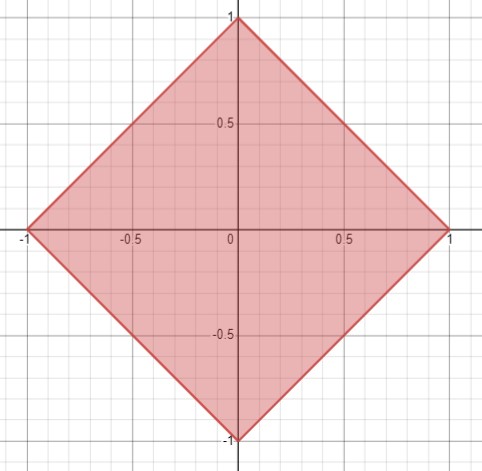
Рассмотрим неравенство \(|x|+|y| \leq 1 \) при различных условиях для переменных \(x \) и \(y \).
1) Пусть \(x \geq 0 \) и \(y \geq 0 \). Тогда получаем систему неравенств:
\(x+y \leq 1\)
\(y \leq -x+1\)
2) Если \(x < 0 \) и \(y \geq 0 \), то система неравенств принимает вид:
\(-x+y \leq 1\)
\(y \leq x+1\)
3) При условии \(x < 0 \) и \(y < 0 \) система неравенств имеет вид:
\(-x-y \leq 1\)
\(y \geq -x-1\)
4) Если \(x \geq 0 \) и \(y < 0 \), то система неравенств записывается как:
\(x-y \leq 1\)
\(y \geq x-1\)
Таким образом, графически множество решений неравенства ограничено прямыми \(y=-x+1 \), \(y=x+1 \), \(y=-x-1 \), \(y=x-1 \).