§8. Неравенства с двумя переменными и их системы — Дополнительные упражнения к параграфу 8 — 522 — стр. 148

Рассмотрим систему неравенств:

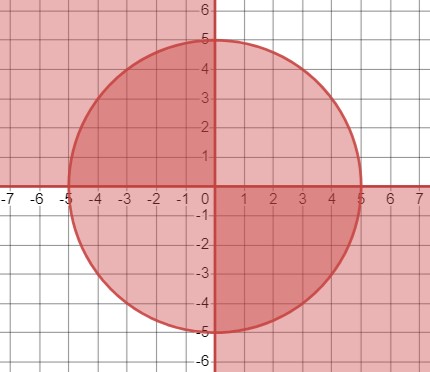
\(\begin{cases}x^2 + y^2 \leq 25 \\x y \leq 0\end{cases}\)

Можем рассмотреть два случая:

1. Когда \(x \geq 0 \) и \(y \leq 0 \):

\(\begin{cases}x^2 + y^2 \leq 25 \\x \geq 0 \\y \leq 0\end{cases}\)

2. Или когда \(x \leq 0 \) и \(y \geq 0 \):

\(\begin{cases}x^2 + y^2 \leq 25 \\x \leq 0 \\y \geq 0\end{cases}\)

Где \(x^2 + y^2 = 25 \) представляет собой окружность с центром в начале координат и радиусом 5.

Аналогично рассмотрим систему неравенств:

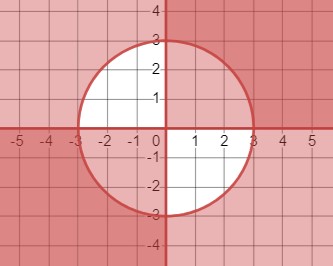
\(\begin{cases}x^2 + y^2 \geq 9 \\x y \geq 0\end{cases}\)

Предлагаем два возможных варианта:

1. Когда \(x \geq 0 \) и \(y \geq 0 \):

\(\begin{cases}x^2 + y^2 \geq 9 \\x \geq 0 \\y \geq 0\end{cases}\)

2. Или когда \(x \leq 0 \) и \(y \leq 0 \):

\(\begin{cases}x^2 + y^2 \geq 9 \\x \leq 0 \\y \leq 0\end{cases}\)

Где \(x^2 + y^2 = 9 \) представляет собой окружность с центром в начале координат и радиусом 3.