§9. Арифметическкая прогрессия — 26.Последовательности — 538 — стр. 152

Рассмотрим неравенство \(x^2 + x - 42 \leq 0\). Построим график функции \(y(x) = x^2 + x - 42\), которая представляет собой параболу с ветвями, направленными вверх. Теперь решим уравнение \(x^2 + x - 42 = 0\):

\(x_{1,2} = \frac{-1 \pm \sqrt{1 + 168}}{2}\)

\(x_1 = 6, \quad x_2 = -7\)

Таким образом, корни уравнения \(x^2 + x - 42 = 0\) равны \(x_1 = 6\) и \(x_2 = -7\). Теперь определим знак выражения \(x^2 + x - 42\) на интервалах, разбивая пространство чисел на отрезки, определяемые корнями уравнения. Получаем интервал \(-7 \leq x \leq 6\).

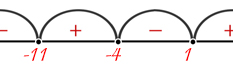
Рассмотрим неравенство \((x + 11)(x + 4)(x - 1) > 0\). Найдем корни уравнения \((x + 11)(x + 4)(x - 1) = 0\):

\(x_1 = -11, \quad x_2 = -4, \quad x_3 = 1\)

Теперь используем метод интервалов: разделим пространство чисел на интервалы, определенные корнями уравнения. Получаем интервалы \((-11, -4)\) и \((1, +\infty)\). Таким образом, решение неравенства - \(x \in (-11, -4) \cup (1, +\infty)\).