§9. Арифметическкая прогрессия — 28. Формула суммы первых n членов арифметической прогрессии — 588 — стр. 166

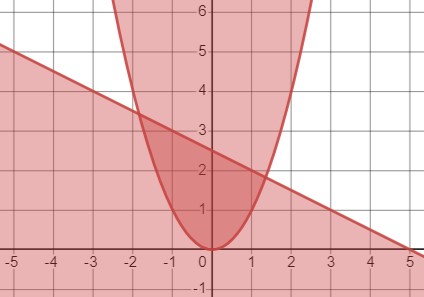
Рассмотрим систему неравенств:
\( \begin{cases}y \geq x^2 \\2y + x \leq 5\end{cases}\)
\(\begin{cases}y \geq x^2 \\y \leq \frac{5-x}{2}\end{cases}\)
Для начала рассмотрим первое уравнение \(y \geq x^2\). Это неравенство описывает область под параболой \(y = x^2\)
Второе уравнение \(y \leq \frac{5-x}{2}\) ограничивает область под графиком прямой.
Таким образом, множество точек, заключённых между графиками \(y = x^2\) и \(y = \frac{5-x}{2}\), включая точки, принадлежащие графикам, описывается системой:
\( \begin{cases}y \geq x^2 \\y \leq \frac{5-x}{2}\end{cases}\)
Это множество включает в себя область, ограниченную графиками.