Постройте график функции:
a) \(y = -2.5x\);
б) \(y = 2x - 3\);
в) \(y = -5\);
г) \(y = -x + 4\);
д) \(y = \frac{1}{2}x + 3\);
e) \(y = \frac{2 - x}{4}\).
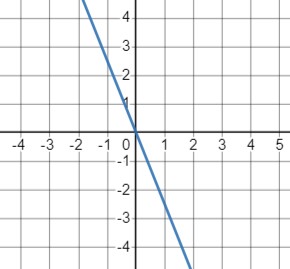
\(y = -2.5x\)
- Это уравнение линейной функции, где коэффициент угла наклона равен -2.5.
- Область определения \(x \in \mathbb{R}\) что означает, что функция определена для любого \(x\).
- Область значений \(y \in \mathbb{R}\) что также означает, что функция может принимать любые значения.
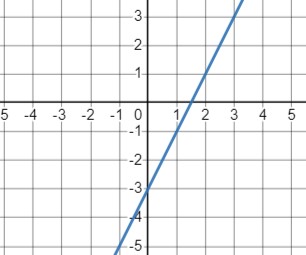
\(y = 2x-3\)
- Область определения \(x \in \mathbb{R}\) что означает, что функция определена для любого \(x\).
- Область значений \(y \in \mathbb{R}\) что также означает, что функция может принимать любые значения.
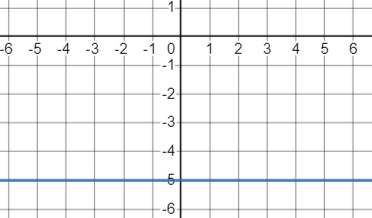
\(y = -5\)
- Это горизонтальная линия, поскольку значение \(y\) постоянно и равно -5.
- Область определения снова \(x \in \mathbb{R}\) а область значений - \(y = -5\).
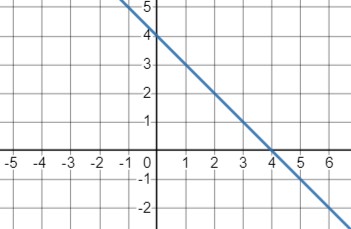
\(y = -x + 4\)
- Еще одна линейная функция с наклоном -1 и константой 4.
- Область определения и область значений - \(\mathbb{R}\).
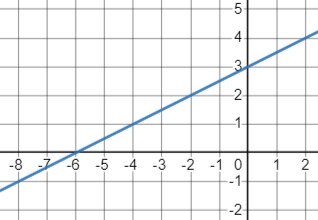
\(y = \frac{1}{2}x + 3\)
- Еще одна линейная функция, но с положительным коэффициентом угла наклона.
- Область определения и область значений - \(\mathbb{R}\).
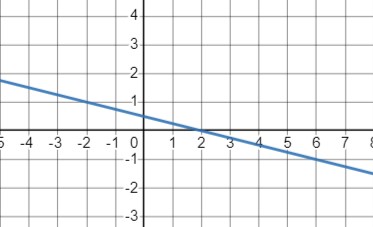
\(y = \frac{2 - x}{4}\)
- Эта функция также линейная, но с коэффициентом угла наклона -1/4 и константой 1/2.
- Область определения и область значений - \(\mathbb{R}\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Постройте график функции: a) \(y = -2.5x\); б) \(y = 2x - 3\); в) \(y = -5\); г) \(y = -x + 4\); д) \(y = \frac{1}{2}x + 3\); e) \(y = \frac{2 - x}{4}\).

