Полярная звезда
2016
Функция \(y = f(x)\) задана формулой \(y = \frac{6 - 2x}{3}\). При каких значениях аргумента \(x\):
a) \(f(x) = 0\);
б) \(f(x) < 0\);
в) \(f(x) \geq 0\)?
Постройте график этой функции.
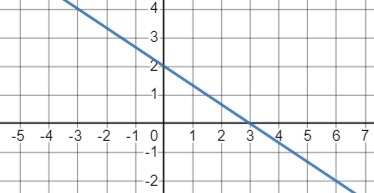
Таблица значений функции \(y=\frac{6-2x}{3}\) для \(x=0, 1.5, 3\) показывает, что при \(x=0\) функция принимает значение \(y=2\) при \(x=1.5\) -> \(y=1\) а при \(x=3\) -> \(y=0\).
а
\(\frac{6-2x}{3}=0\)
- Решение уравнения \(6-2x=0\) привело к \(x=3\). Это точка, в которой функция равна нулю.
б
\(\frac{6-2x}{3}<0\)
- Решение неравенства \(6-2x<0\) привело к \(x>3\). Это говорит нам о том, что функция отрицательна для значений \(x>3\).
в
\(\frac{6-2x}{3}\geq0\)
- Решение неравенства \(6-2x\geq0\) привело к \(x\leq3\). Это говорит нам о том, что функция неотрицательна для значений \(x\leq3\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Функция \(y = f(x)\) задана формулой \(y = \frac{6 - 2x}{3}\). При каких значениях аргумента \(x\): a) \(f(x) = 0\); б) \(f(x) < 0\); в) \(f(x) \geq 0\)? Постройте график этой функции.
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
