Упражнении дли повторении курса 7-9 классов — Функции — 823 — стр. 207

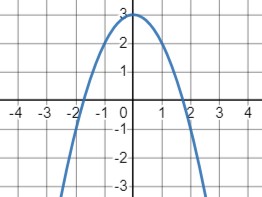
Уравнение \(y = -x^2 + 3\) представляет собой квадратичную функцию с вершиной в точке \((0, 3)\) и направленной вниз, так как коэффициент при \(x^2\) отрицательный.
1) Когда \(y = -1\) решение уравнения \( -x^2 + 3 = -1\) даёт два корня \(x = \pm 2\). Таким образом, точки \((-2, -1)\) и \((2, -1)\) лежат на графике функции.
2) Когда \(y = 1\) решение \( -x^2 + 3 = 1\) дает \(x = \pm\sqrt{2}\).
3) Когда \(y = 5\) уравнение \( -x^2 + 3 = 5\) не имеет вещественных корней, что подтверждено анализом уравнения.
График демонстрирует, что функция имеет вершину в точке \((0, 3)\). Таким образом, область определения \(x\) — это все вещественные числа, а область значений \(y\) — это интервал \((-\infty, 3]\).