Упражнении дли повторении курса 7-9 классов — Функции — 824 — стр. 207

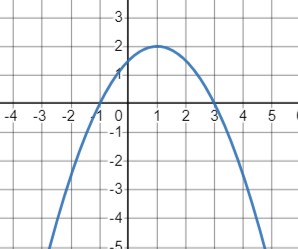
1. Нахождение нулей функции (\(y = 0\)):
\(-0,5x^2 + x + 1,5 = 0\)
\(x^2 - 2x - 3 = 0\)
Решив квадратное уравнение, получаем \(x_1 = 3\) и \(x_2 = -1\)
2. Определение знака функции (\(y > 0, y < 0\)):
- \(y > 0\) для \(x \in (-1; 3)\)
- \(y < 0\) для \(x \in (-\infty; -1) \cup (3; +\infty)\)
3. Нахождение координат вершины параболы:
Используя формулу \(x_0 = -\frac{b}{2a}\) находим вершину \(x_0 = 1\). Подставив \(x_0\) в уравнение функции, получаем \(y(1) = 2\).
4. Исследование возрастания и убывания функции:
- Функция возрастает на \((-\infty; 1)\)
- Функция убывает на \((1; +\infty)\)
5. Нахождение максимального значения функции:
Максимальное значение достигается в вершине параболы при \(x = 1\) и равно \(y = 2\)
Таким образом, проведенное исследование позволяет понять основные характеристики функции и её поведение на числовой оси.