Упражнении дли повторении курса 7-9 классов — Функции — 825 — стр. 207

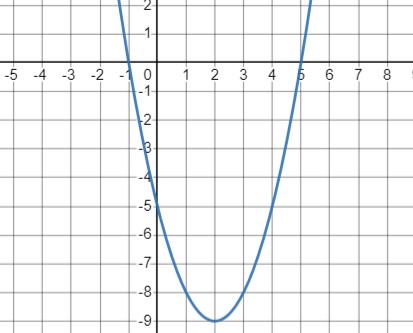
Заданная функция \(y = x^2 - 4x - 5\) представляет собой квадратичную параболу с ветвями, направленными вверх.
1. Таблица значений:
- При \(x = -2\) \(y = 7\)
- При \(x = 0\) \(y = -5\)
- При \(x = 2\) \(y = -9\)
2. График параболы:
- Парабола имеет ветви, направленные вверх, что согласуется с уравнением.
- Подставив указанные значения \(x\) в уравнение функции, получаем соответствующие значения \(y\)
3. Определение знака функции:
- \(y < 0\) при \(x \in (-1; 5)\). Это указывает на то, что парабола на этом интервале находится под осью \(X\)
4. Интервал, где \(y\) находится в заданном диапазоне:
- При \(x \in (0; 4)\) \(y \in (-9; -5)\). Таким образом, на этом интервале значения \(y\) находятся в заданном диапазоне.