Упражнении дли повторении курса 7-9 классов — Функции — 826 — стр. 207

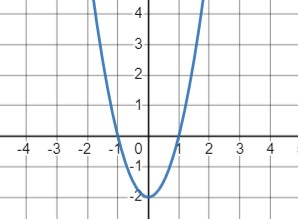
График функции \(y = 2x^2 - 2\):

- Парабола с ветвями, направленными вверх.

Значения функции:

- При \(x = 0\) \(y = -2\) наименьшее значение функции.

- При \(x = 1\) \(y = 0\)

- При \(x = 2\) \(y = 6\)

- Вершина параболы находится в точке \((0, -2)\).

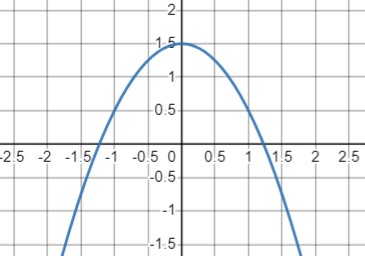
График функции \(y = -x^2 + 1.5\):

- Парабола с ветвями, направленными вниз.

Значения функции:

- При \(x = 0\) \(y = 1.5\) наибольшее значение функции.

- При \(x = 1\) \(y = 0.5\)

- При \(x = 2\) \(y = -2.5\)

- Вершина параболы находится в точке \((0, 1.5)\).

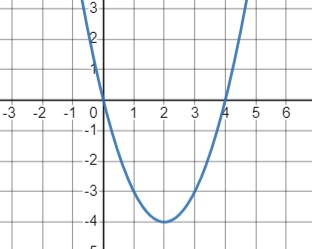
График функции \(y = x^2 - 4x\):

- Парабола с ветвями, направленными вверх.

Значения функции:

- При \(x = 0\) \(y = 0\)

- При \(x = 1\) \(y = -3\)

- При \(x = 2\) \(y = -4\) наименьшее значение функции.

- Вершина параболы находится в точке \((2, -4)\).

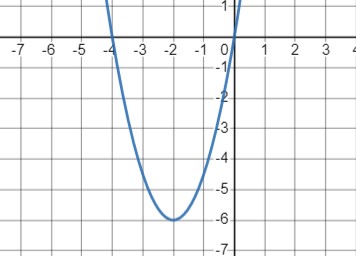
График функции \(y = 1.5x^2 + 6x\):

- Парабола с ветвями, направленными вверх.

Значения функции:

- При \(x = -2\) \(y = -6\) наименьшее значение функции.

- При \(x = 0\) \(y = 0\)

- При \(x = 1\) \(y = 7.5\)

- Вершина параболы находится в точке \((-2, -6)\).

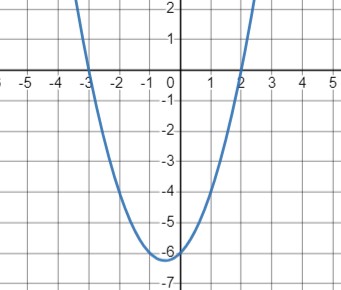
График функции \(y = x^2 + x - 6\):

- Парабола с ветвями, направленными вверх.

Значения функции:

- При \(x = 0.25\) \(y = -6.25\) наименьшее значение функции.

- При \(x = 1\) \(y = -4\)

- При \(x = 2\) \(y = 0\)

- Вершина параболы находится в точке \((-\frac{1}{2}, -6\frac{1}{4}\).

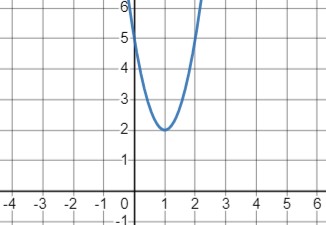
График функции \(y = 3x^2 - 6x + 5\):

- Парабола с ветвями, направленными вверх.

Значения функции:

- При \(x = 0\) \(y = 5\)

- При \(x = 1\) \(y = 2\) наименьшее значение функции.

- При \(x = 2\) \(y = 5\)

- Вершина параболы находится в точке \((1, 2)\).