Упражнении дли повторении курса 7-9 классов — Функции — 828 — стр. 207

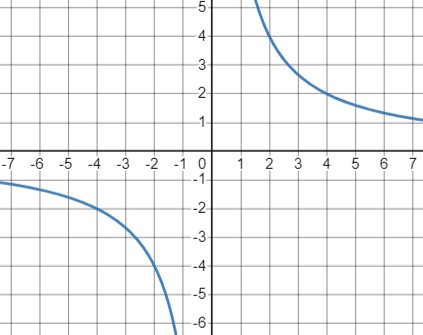
\(y=\frac{8}{x}\):

- Область определения: \(x \neq 0\)

- Таблица значений показывает, что функция принимает положительные значения, когда \(x > 0\) и отрицательные значения, когда \(x < 0\)

- График функции: Гипербола с вертикальными асимптотами на \(x = 0\). Функция стремится к бесконечности при \(x \to 0\) справа и к минус бесконечности при \(x \to 0\) слева.

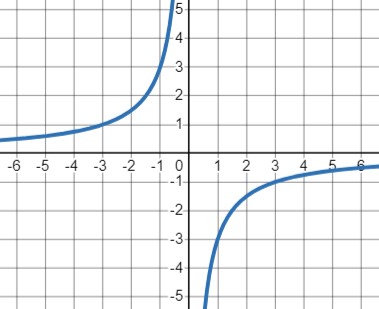
\(y=-\frac{3}{x}\):

- Область определения: \(x \neq 0\)

- Таблица значений также показывает, что функция принимает положительные значения, когда \(x < 0\) и отрицательные значения, когда \(x > 0\)

- График функции: Гипербола с вертикальными асимптотами на \(x = 0\). Зеркальное отражение графика предыдущей функции \(\frac{8}{x}\) относительно оси \(y\)

Обе функции имеют вертикальные асимптоты в точке \(x = 0\) что соответствует области определения, и оба графика симметричны относительно оси \(y\).