Упражнении дли повторении курса 7-9 классов — Функции — 829 — стр. 207

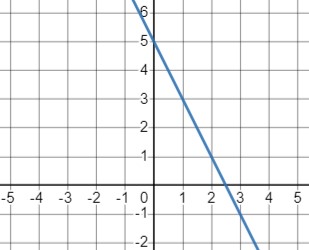
\(y=ax+5\) при \(a<0\):

- При \(a<0\) линейная функция \(y=ax\) является убывающей. Добавление константы 5 приводит к смещению графика вверх по оси \(y\).

- Функция представляет собой наклонную прямую, и её график будет пересекать ось \(y\) в точке (0, 5).

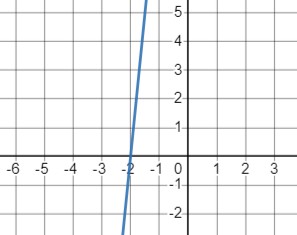
\(y=10x+b\) при \(b>0\):

- Функция представляет собой увеличенную на 10 и смещенную вверх на \(b\) единиц вертикальную прямую.

- При \(b>0\) график функции будет пересекать ось \(y\) в точке (0, \(b\)).

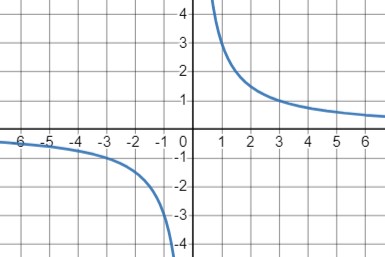
\(y=\frac{k}{x}\) при \(k>0\):

- Область определения: \(x \neq 0\). Функция представляет собой гиперболу в первой и третьей четвертях.

- График будет стремиться к положительной бесконечности при \(x \to 0^+\) и к отрицательной бесконечности при \(x \to 0^-\).

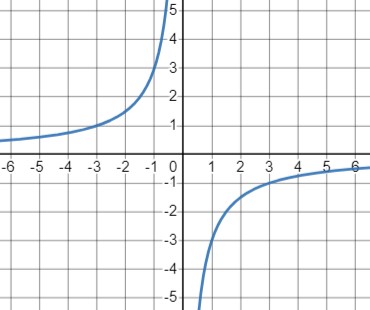
\(y=\frac{k}{x}\) при \(k<0\):

- Область определения: \(x \neq 0\). График гиперболы будет во второй и четвёртой четвертях.

- Функция будет стремиться к отрицательной бесконечности при \(x \to 0^+\) и к положительной бесконечности при \(x \to 0^-\).

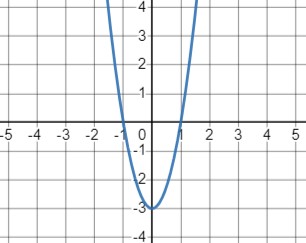
\(y=ax^2-3\) при \(a>0\):

- При \(a>0\) ветви параболы направлены вверх. Смещение графика вниз на 3 единицы.

- Функция представляет собой параболу с вершиной в точке (0, -3).

\(y=ax^2+2\) при \(a<0\):

- При \(a<0\) ветви параболы направлены вниз. Смещение графика вверх на 2 единицы.

- Функция представляет собой параболу с вершиной в точке (0, 2).

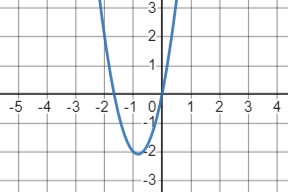
\(y=ax^2+bx\) при \(a>0, b>0\):

- При \(a>0\) ветви параболы направлены вверх. Координаты вершины параболы \(x_0=-\frac{b}{2a}\).

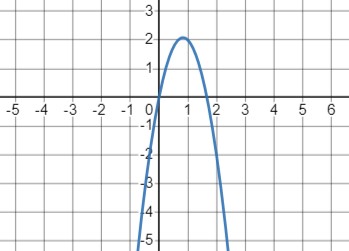
\(y=ax^2+bx\) при \(a<0, b>0\):

- При \(a<0\) ветви параболы направлены вниз. Координаты вершины параболы \(x_0=-\frac{b}{2a}\).