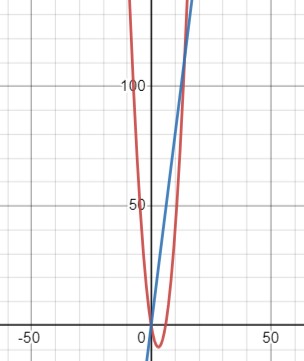
Пересекаются ли парабола \(y = x^2 - 6x\) и прямая \(y - 8x = 0\)? Если да, то укажите координаты точек пересечения. Проиллюстрируйте ответ с помощью схематического рисунка.
\(\begin{cases}y = x^2 - 6x \\ y - 8x = 0\end{cases}\)
Приводим систему к уравнению:
\(\begin{cases}x^2 - 6x = 8x \\ y = 8x\end{cases}\)
\(\begin{cases}x^2 - 14x = 0 \\ y = 8x\end{cases}\)
Решаем уравнение \(x^2 - 14x = 0\) получаем два корня \(x = 0\) и \(x = 14\)
Подставляем найденные значения обратно в уравнение системы, чтобы найти соответствующие значения \(y\):
\(\begin{cases}x = 0 \\ y = 8 \cdot 0\end{cases} \Rightarrow (0, 0) \\ \begin{cases}x = 14 \\ y = 8 \cdot 14\end{cases} \Rightarrow (14, 112)\)
Таким образом, правильные точки пересечения уравнений \(y = x^2 - 6x\) и \(y - 8x = 0\) - это \((0, 0)\) и \((14, 112)\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Пересекаются ли парабола \(y = x^2 - 6x\) и прямая \(y - 8x = 0\)? Если да, то укажите координаты точек пересечения. Проиллюстрируйте ответ с помощью схематического рисунка.

