Spotlight
2024
Изобразив схематически графики, выясните, имеет ли уравнение корни:
а) \(\frac{1}{2} x-2=x^{3}\);
б) \(-3 x-1=\sqrt{x}\);
в) \(\frac{1}{x}=-x^{2}+1\);
г) \(3+x^{2}=\frac{12}{x}\).
а
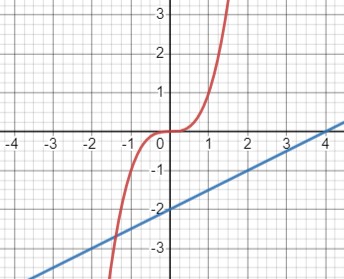
\(\frac{1}{2}x - 2 = x^3\)
Рассмотрим графики двух функций: \(y = \frac{1}{2}x - 2\) (синий график) и \(y = x^3\) (красный график).
Сначала определим область определения. Для обеих функций она равна \(x \in \mathbb{R}\)
Теперь заполним таблицы значений для обеих функций:
\(\begin{cases}\hline x & 0 & 1 & 2 \\ \hline y (\frac{1}{2}x - 2) & -2 & -1.5 & -1 \\ \hline\end{cases}\)
\(\begin{cases}\hline x & 0 & 1 & 2 \\ \hline y (x^3) & 0 & 1 & 8 \\ \hline\end{cases}\)
Графики пересекаются в одной точке, следовательно, уравнение имеет один корень.
б
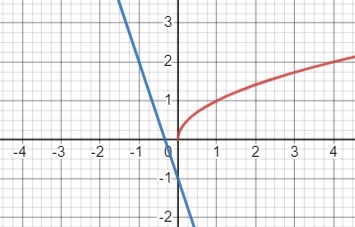
\(-3x - 1 = \sqrt{x}\)
Рассмотрим графики двух функций: \(y = -3x - 1\) (синий график) и \(y = \sqrt{x}\) (красный график).
Определим область определения для обеих функций: \(x \in \mathbb{R}\) для синего графика и \(x \geq 0\) для красного графика.
Теперь заполним таблицы значений:
\(\begin{cases}\hline x & -1 & 0 & 1 \\ \hline y (-3x - 1) & 2 & -1 & -4 \\ \hline\end{cases}\)
\(\begin{cases}\hline x & 0 & 1 & 4 \\ \hline y (\sqrt{x}) & 0 & 1 & 2 \\ \hline\end{cases}\)
Графики не пересекаются, поэтому уравнение не имеет корней.
в
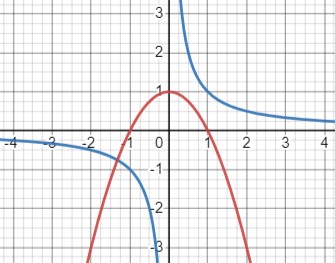
\(\frac{1}{x} = -x^2 + 1\)
Рассмотрим графики двух функций: \(y = \frac{1}{x}\) (синий график) и \(y = -x^2 + 1\) (красный график).
Определим область определения для обеих функций: \(x \neq 0\) для синего графика и \(x \in \mathbb{R}\) для красного графика.
Теперь заполним таблицы значений:
\(\begin{cases}\hline x & -1 & 1 & 2 \\ \hline y (\frac{1}{x}) & -1 & 1 & 0.5 \\ \hline\end{cases}\)
\(\begin{cases}\hline x & 0 & 1 & 2 \\ \hline y (-x^2 + 1) & 0 & 0 & -3 \\ \hline\end{cases}\)
Графики пересекаются в одной точке, следовательно, уравнение имеет один корень.
г
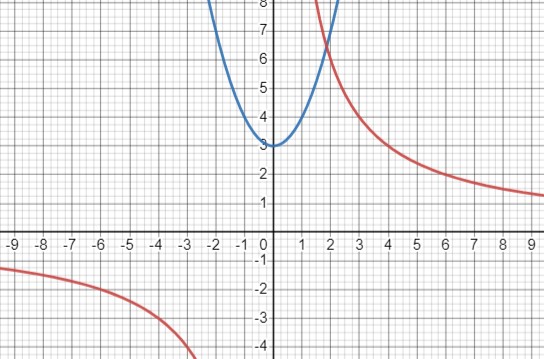
\(3 + x^2 = \frac{12}{x}\)
Рассмотрим графики двух функций: \(y = 3 + x^2\) (синий график) и \(y = \frac{12}{x}\) (красный график).
Определим область определения для обеих функций: \(x \in \mathbb{R}\) для синего графика и \(x \neq 0\) для красного графика.
Теперь заполним таблицы значений:
\(\begin{cases}\hline x & 0 & 1 & 2 \\ \hline y (3 + x^2) & 3 & 4 & 7 \\ \hline\end{cases}\)
\(\begin{cases}\hline x & -4 & 3 & 4 \\ \hline y (\frac{12}{x}) & -3 & 4 & 3 \\ \hline\end{cases}\)
Графики пересекаются в одной точке, следовательно, уравнение имеет один корень.
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Изобразив схематически графики, выясните, имеет ли уравнение корни: а) \(\frac{1}{2} x-2=x^{3}\); б) \(-3 x-1=\sqrt{x}\); в) \(\frac{1}{x}=-x^{2}+1\); г) \(3+x^{2}=\frac{12}{x}\).
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
