Упражнении дли повторении курса 7-9 классов — Уравнения и системы уравнений — 769 — стр. 199

Система уравнений:

\(\begin{cases}y+x^2=5 x \\ 2 y+5=x\end{cases}\)

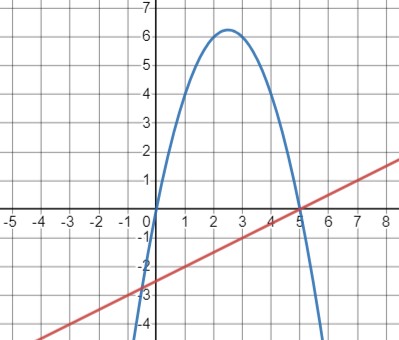
Первое уравнение можно переписать в виде \(y = 5x - x^2\) а второе как \(y = \frac{x-5}{2}\)

Графики двух уравнений:

- Синий график: \(y = 5x - x^2\)

\(\frac{x}{y}|\frac{1}{4}|\frac{2}{6}|\frac{3}{6}\)

- Красный график: \(y = \frac{x-5}{2}\)

\(\frac{x}{y}|\frac{-1}{-3}|\frac{1}{-2}|\frac{3}{-1}\)

Две точки пересечения графиков - два решения \((-0.5, -2.75)\) и \((5, 0)\).

Система уравнений:

\(\begin{cases}x^2+y^2=25 \\ 2 x^2+y=6\end{cases}\)

\(\begin{cases}x^2+y^2=25 \\ y = 6 - 2x^2\end{cases}\)

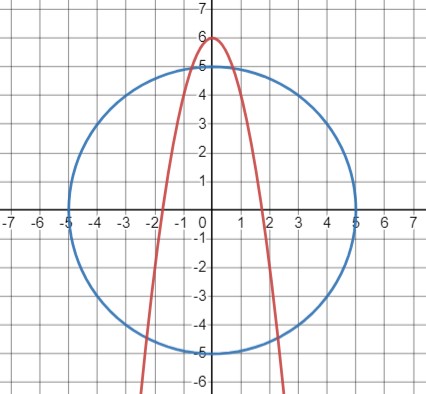
Графики двух уравнений:

- Синий график: \(x^2+y^2=25\) (окружность с центром в начале координат и радиусом 5)

- Красный график: \(y = 6 - 2x^2\)

\(\frac{x}{y}|\frac{0}{6}|\frac{1}{4}|\frac{2}{-2}\)

Четыре точки пересечения графиков - четыре решения системы уравнений.

Система уравнений:

\(\begin{cases}xy=1 \\ x^2+y^2=9\end{cases}\)

\(\begin{cases}y=\frac{1}{x}\\ x^2+y^2=9\end{cases}\)

Графики двух уравнений:

- Синий график: \(y = \frac{1}{x}\)

\(\frac{x}{y}|\frac{-1}{-1}|\frac{1}{1}|\frac{2}{0.5}\)

- Красный график: \(x^2+y^2=9\) (окружность с центром в начале координат и радиусом 3)

Четыре точки пересечения графиков - четыре решения системы уравнений.

Система уравнений:

\(\begin{cases}xy=-2 \\ y+8=\frac{1}{2}x^2\end{cases}\)

\(\begin{cases}y = -\frac{2}{x} \\ y = \frac{1}{2}x^2-8\end{cases}\)

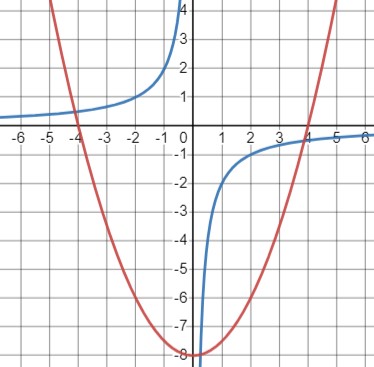
Графики двух уравнений:

- Синий график: \(-\frac{2}{x}\)

\(\frac{x}{y}|\frac{-1}{2}|\frac{1}{-2}|\frac{2}{-1}\)

- Красный график: \(y = \frac{1}{2}x^2-8\)

\(\frac{x}{y}|\frac{0}{-8}|\frac{2}{-6}|\frac{4}{0}\)

Три точки пересечения графиков - три решения системы уравнений.