Упражнении дли повторении курса 7-9 классов — Задачи повышенной трудности — 841 — стр. 209

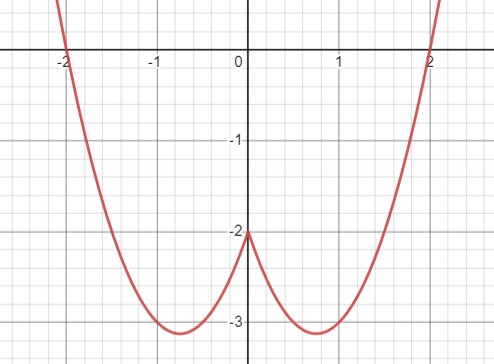
Рассмотрим уравнение \(y=2x^2-3|x|-2\).

Для \(x\geq0\) -> \(y=2x^2-3x-2 \) а для \(x<0\) -> \(y=2x^2+3x-2 \). Таким образом, график состоит из правой части \(y=2x^2-3x-2\) при \(x\geq0\) и левой части \(y=2x^2+3x-2\) при \(x<0\).

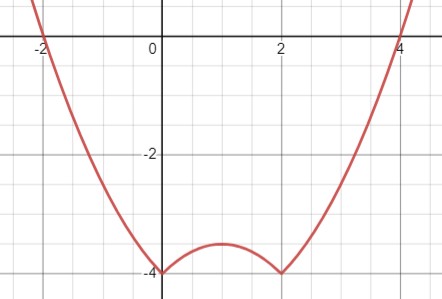
Рассмотрим уравнение \(y=\left|\frac{1}{2}x^2-x\right|-4\).

Решим неравенство \(\frac{1}{2}x^2-x\geq0:\)

\(x^2-2x\geq0\)

\(x(x-2)\geq0\)

Решение неравенства: \(x\in(-\infty;0]\cup[2;+\infty)\)

Далее, рассмотрим случаи \(\frac{1}{2}x^2-x<0:\)

\(x^2-2x<0\)

\(x(x-2)<0\)

Решение неравенства: \(x\in(0;2)\)

Таким образом, уравнение разбивается на два случая:

\(\begin{cases}y=\frac{1}{2}x^2-x-4, \text{ при } x\in(-\infty;0]\cup[2;+\infty) \\ y=-\frac{1}{2}x^2+x-4, \text{ при } x\in(0;2)\end{cases}\).