Линия жизни
2016
Изобразите множество решений неравенства:
а) \(y \leq \frac{10}{|x|}\);
б) \(y + \left|\frac{8}{x}\right| \geq 0\);
в) \(|y| - x^2 + 2x \leq 1\);
г) \(|y| + x^2 - 4x \geq 4\).
а
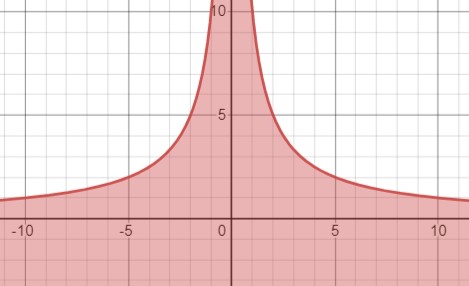
Рассмотрим неравенство \(y \leq \frac{10}{|x|}\). Преобразуем его к виду \(\begin{cases} x < 0 \\ y \leq -\frac{10}{x} \end{cases}\) или \(\begin{cases} x > 0 \\ y \leq \frac{10}{x} \end{cases}\). Множество решений - это область под левой веткой гиперболы \(y=-\frac{10}{x}\) и под правой веткой гиперболы \(y=\frac{10}{x}\) включая сами ветки.
б
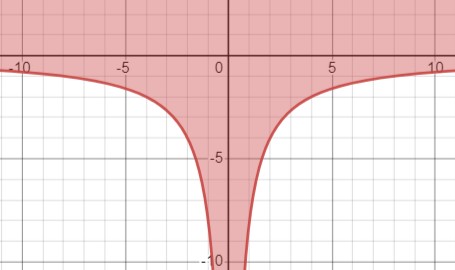
Рассмотрим неравенство \(y + \left|\frac{8}{x}\right| \geq 0\). Преобразуем его к виду \(\begin{cases} x < 0 \\ y \geq \frac{8}{x} \end{cases}\) или \(\begin{cases} x > 0 \\ y \geq -\frac{8}{x} \end{cases}\). Множество решений - это область над левой веткой гиперболы \(y=\frac{8}{x}\) и над правой веткой гиперболы \(y=-\frac{8}{x}\) включая сами ветки.
в
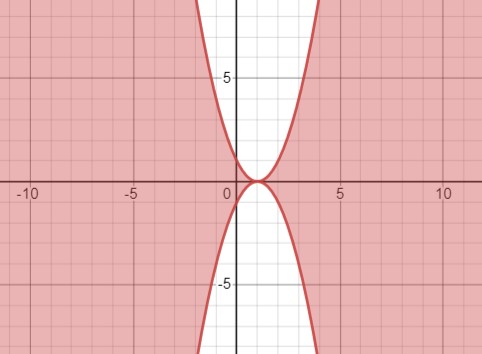
Рассмотрим неравенство \(|y| - x^2 + 2x \leq 1\). Преобразуем его к виду \(\begin{cases} y < 0 \\ y \geq -(x-1)^2 \end{cases}\) или \(\begin{cases} y \geq 0 \\ y \leq (x-1)^2 \end{cases}\). В верхней полуплоскости область под параболой \(y=(x-1)^2\) в нижней полуплоскости область над параболой \(y=-(x-1)^2\) включая сами параболы.
г
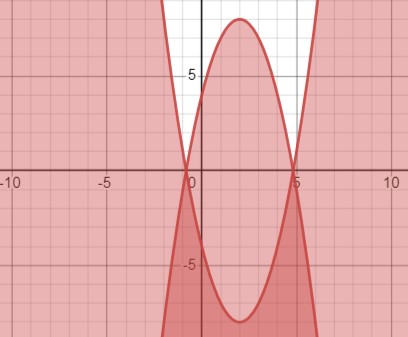
Рассмотрим неравенство \(|y| + x^2 - 4x \geq 4\). Преобразуем его к виду \(\begin{cases} y < 0 \\ y \leq (x-2)^2 - 8 \end{cases}\) или \(\begin{cases} y \geq 0 \\ y \geq -(x-2)^2 + 8 \end{cases}\). В верхней полуплоскости область над параболой \(y=-(x-2)^2+8\) в нижней полуплоскости область под параболой \(y=(x-2)^2-8\), включая сами параболы.
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Изобразите множество решений неравенства: а) \(y \leq \frac{10}{|x|}\); б) \(y + \left|\frac{8}{x}\right| \geq 0\); в) \(|y| - x^2 + 2x \leq 1\); г) \(|y| + x^2 - 4x \geq 4\).
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
