Упражнении дли повторении курса 7-9 классов — Задачи повышенной трудности — 893 — стр. 214

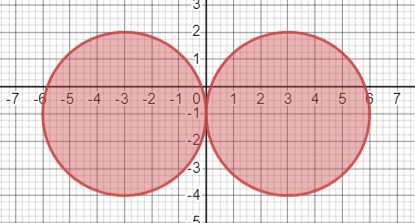
Рассмотрим неравенство \(x^2+y^2-6|x|+2y \leq -1\). Преобразуем его:

\((x^2-6|x|+9) + (y^2+2y+1) \leq -1 + 9 + 1\)

\((|x|-3)^2 + (y+1)^2 \leq 9\)

Это неравенство можно представить в виде двух случаев:

1. Когда \(x < 0\): \((x+3)^2 + (y+1)^2 \leq 9\)

2. Когда \(x \geq 0\): \((x-3)^2 + (y+1)^2 \leq 9\)

Множество решений представляет собой два круга радиусом 3 с центрами в точках \((-3, -1)\) и \((3, -1)\) касающимися в точке \((0, -1)\). Границы этих кругов включены в множество решений.

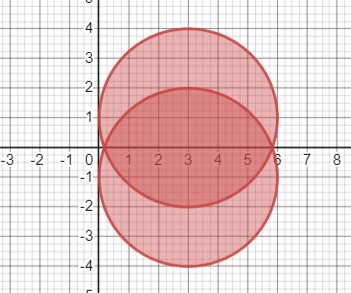
Рассмотрим неравенство \(x^2+y^2-6x+2|y| \leq -1\). Преобразуем его:

\((x^2-6x+9) + (y^2+2|y|+1) \leq -1 + 9 + 1\)

\((x-3)^2 + (|y|-1)^2 \leq 9\)

Это неравенство можно представить в виде двух случаев:

1. Когда \(y < 0\): \((x-3)^2 + (y-1)^2 \leq 9\)

2. Когда \(y \geq 0\): \((x-3)^2 + (y+1)^2 \leq 9\)

Множество решений представляет собой сегмент \(y \geq 0\) круга радиусом 3 с центром в точке \((3, -1)\) и сегмент \(y < 0\) круга радиусом 3 с центром в точке \((3, 1)\). Границы этих сегментов включены в множество решений.