Упражнении дли повторении курса 7-9 классов — Задачи повышенной трудности — 894 — стр. 214

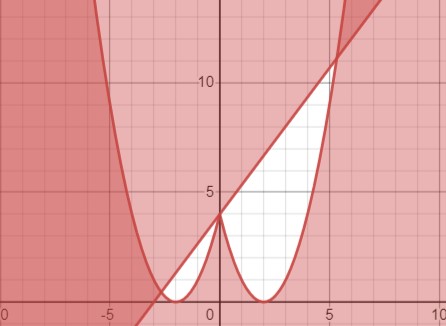
Рассмотрим систему неравенств:
\(\begin{cases}y - 4 \leq x^2 - 4|x| \\ 4x - 3y \leq -12\end{cases}\)
Преобразуем её для удобства:
\(\begin{cases}y \leq x^2 - 4|x| + 4 \\ 4x + 12 \leq 3y\end{cases}\)
Система примет вид:
\(\begin{cases}y \leq (|x| - 2)^2 \\ y \geq \frac{4}{3}x + 4\end{cases}\)
Множество решений будет представлять собой область под графиком параболы \(y=(|x|-2)^2\) и над прямой \(y=\frac{4}{3}x + 4\), а также включать точку \((0,4)\). Границы входят в множество решений.