Изобразите множество решений системы неравенств:
а) \(\left\{\begin{array}{l}x^2 + y^2 \leq 9, \\ |x| + |y| \leq 0.\end{array}\right.\)
б) \(\left\{\begin{array}{l}x^2 + y^2 \leq 9, \\ |y| - |x| \leq 0.\end{array}\right.\)
а
Рассмотрим систему неравенств:
\(\begin{cases}x^2 + y^2 \leq 9 \\ |x| + |y| \leq 0\end{cases}\)
Преобразуем второе неравенство:
\(|x| + |y| = 0\)
\(x = 0, y = 0\)
Таким образом, система упрощается:
\(\begin{cases}x^2 + y^2 \leq 9 \\ x = y = 0\end{cases}\)
Искомое решение - точка \((0, 0)\) которая также удовлетворяет первому неравенству.
б
Теперь рассмотрим систему:
\(\begin{cases}x^2 + y^2 \leq 9 \\ |y| - |x| \leq 0\end{cases}\)
Преобразуем второе неравенство:
\(|y| - |x| = 0\)
\(|y| = |x|\)
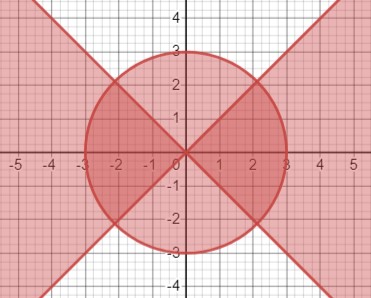
Это означает, что область \(|y| \leq |x|\) представляет собой объединение верхней полуплоскости под ломаной \(y = |x|\) и нижней полуплоскости над ломаной \(y = -|x|\)
Область \(x^2 + y^2 \leq 9\) - это круг радиусом 3 с центром в начале координат.
Итак, искомое множество - это пересечение двух областей: круга и объединения двух полуплоскостей. Границы всех этих фигур входят в множество решений.
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Изобразите множество решений системы неравенств: а) \(\left\{\begin{array}{l}x^2 + y^2 \leq 9, \\ |x| + |y| \leq 0.\end{array}\right.\) б) \(\left\{\begin{array}{l}x^2 + y^2 \leq 9, \\ |y| - |x| \leq 0.\end{array}\right.\)
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
