Алгебра
2023
Площадь круга \(S(\text{см}^{2})\) вычисляется по формуле \(S=\pi r^{2}\), где \(r\) (см) - радиус круга. Постройте график функции \(S=\pi r^{2}\) и найдите по графику:
а) площадь круга, если его радиус равен \(1,3\) см; \(0,8\) см; \(2,1\) см;
б) радиус круга, площадь которого равна \(1,8 \text{ см}^{2}\); \(2,5 \text{ см}^{2}\); \(6,5 \text{ см}^{2}\).
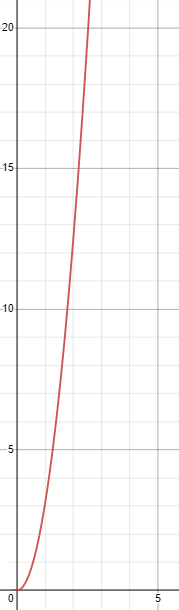
\(S = πr^2\)
\(\frac{x}{y}|\frac{0}{0}|\frac{1}{3,14}|\frac{2}{12,57}|\frac{3}{28,27}\).
а
\( r=1,3 см: S \approx 5,3 см^2 \\r=0,8 см: S \approx 2 см^2 \\ r=2,1 см: S \approx 13,8 см^2\).
б
\( S=1,8 см^2: r \approx 0,7 см \\S=2,5 см^2: r \approx 0,9 см \\ S=6,5 см^2: r \approx 1,4 см\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Площадь круга \(S(\text{см}^{2})\) вычисляется по формуле \(S=\pi r^{2}\), где \(r\) (см) - радиус круга. Постройте график функции \(S=\pi r^{2}\) и найдите по графику: а) площадь круга, если его радиус равен \(1,3\) см; \(0,8\) см; \(2,1\) см; б) радиус круга, площадь которого равна \(1,8 \text{ см}^{2}\); \(2,5 \text{ см}^{2}\); \(6,5 \text{ см}^{2}\).
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
Обществознание
2023