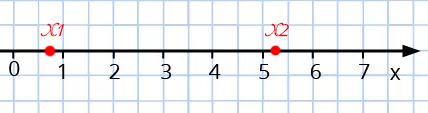
Решите уравнение \((x+3)^{2}-(x-3)^{2}=(x-2)^{2}+(x+2)^{2}\) и отметьте его корни на координатной прямой.
\((x+3)^{2}-(x-3)^{2}=(x-2)^{2}+(x+2)^{2}\\x^{2}+6x+9-x^{2}+6x-9=x^{2}-4x+4+x^{2}+4x+4\\12x=2x^{2}+8\\x^{2}-6x+4=0\\x_{1,2}=\frac{6 \pm \sqrt{36-16}}{2}\\x_{1,2}=3 \pm 2\sqrt{5}\)
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Решите уравнение \((x+3)^{2}-(x-3)^{2}=(x-2)^{2}+(x+2)^{2}\) и отметьте его корни на координатной прямой.
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
