Постройте в одной системе координат графики функций \(y=\frac{1}{3}x^{2}\) и \(y=-\frac{1}{3}x^{2}\). Найдите промежутки возрастания и убывания для каждой функции.
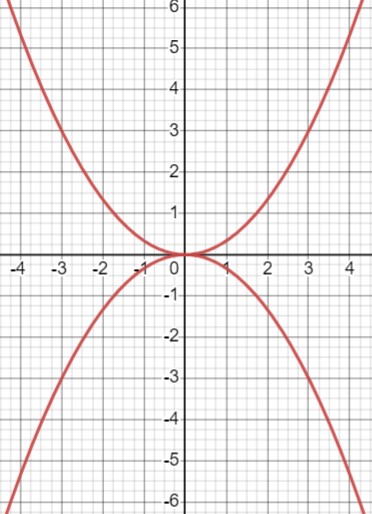
Давайте найдем производные функций \(y = \frac{1}{3}x^2\) и \(y = -\frac{1}{3}x^2\) для определения их поведения.
1
Для \(y = \frac{1}{3}x^2\):
\(y = \frac{d}{dx}\left(\frac{1}{3}x^2\right) = \frac{2}{3}x\)
Промежутки возрастания и убывания определяются знаками производной. Учитывая, что \(\frac{2}{3}\) положительно, функция \(\frac{1}{3}x^2\) возрастает при \(x > 0\) и убывает при \(x < 0\).
2
Для \(y = -\frac{1}{3}x^2\):
\(y = \frac{d}{dx}\left(-\frac{1}{3}x^2\right) = -\frac{2}{3}x\)
Аналогично, учитывая, что \(-\frac{2}{3}\) отрицательно, функция \(-\frac{1}{3}x^2\) возрастает при \(x 0\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Постройте в одной системе координат графики функций \(y=\frac{1}{3}x^{2}\) и \(y=-\frac{1}{3}x^{2}\). Найдите промежутки возрастания и убывания для каждой функции.
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
