§4. Квадратичная функция и ее график — Дополнительные упражнения к параграфу 4 — 205 — стр. 70

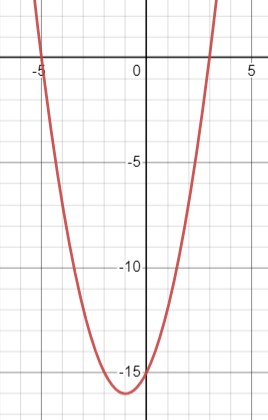
\(y=x^2+2 x-15 \\y=(x^2+2 x+1)-16 \\=(x+1)^2-16\)

Область определения: \(x \in \mathbb{R}\);

Область значений: \(y \in [-16, +\infty)\);

Функция убывает при \(x \in (-\infty, -1]\), функция возрастает при \(x \in [-1, +\infty)\);

Функция не является чётной или нечётной;

\(y 0\) при \(x \in (-\infty, -5) \cup (3, +\infty)\).

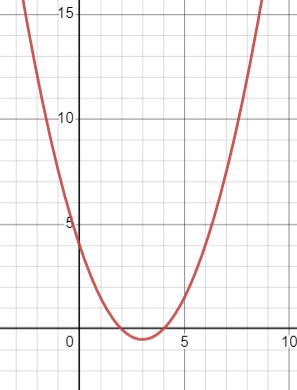
\(y=0.5 x^2-3 x+4 \\y=0.5(x^2-2 \cdot 3 x+9)-0.5 \\=0.5(x-3)^2-0.5\)

Область определения: \(x \in \mathbb{R}\);

Область значений: \(y \in [-0.5, +\infty)\);

Функция убывает при \(x \in (-\infty, 3]\), функция возрастает при \(x \in [3, +\infty)\);

Функция не является чётной или нечётной;

\(y 0\) при \(x \in (-\infty, 2) \cup (4, +\infty)\).

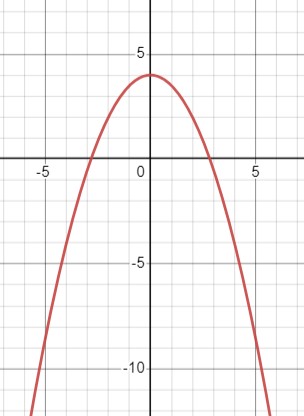
\(y=4-0.5 x^2\)

\(y=-0.5 x^2+4\)

Область определения: \(x \in \mathbb{R}\);

Область значений: \(y \in (-\infty, 4]\);

Функция убывает при \(x \in [0, +\infty)\), функция возрастает при \(x \in (-\infty, 0]\);

Функция чётная.

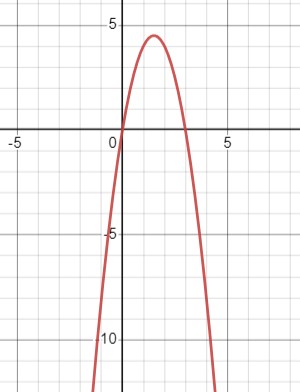
\(y=6 x-2 x^2 \\ y=-2(x^2-2 \cdot 1.5 x+2.25)+4.5 \\=-2(x-1.5)^2+4.5 \)

Область определения: \(x \in \mathbb{R}\);

Область значений: \(y \in (-\infty, 4.5]\);

Функция убывает при \(x \in [1.5, +\infty)\), функция возрастает при \(x \in (-\infty, 1.5]\);

Функция не является чётной или нечётной;

\(y > 0\) при \(x \in (0, 3)\);

\(y < 0\) при \(x \in (-\infty, 0) \cup (3, +\infty)\).

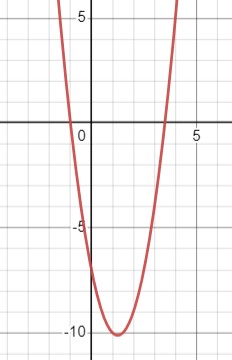
\(y=(2 x-7)(x+1) \\ y=2 x^2-7 x+2 x-7 \\ =2(x^2-2 \cdot 1.25 x+1.25^2)-10.125 \\ =2(x-1.25)^2-10.125 \)

Область определения: \(x \in \mathbb{R}\);

Область значений: \(y \in (-10.125, +\infty)\);

Функция убывает при \(x \in (-\infty, 1.25]\), функция возрастает при \(x \in [1.25, +\infty)\);

Функция не является чётной или нечётной;

\(y 0\) при \(x \in (-\infty, -1) \cup (3.5, +\infty)\).

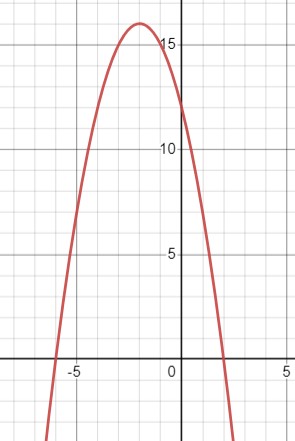
\(y=(2-x)(x+6) \\y=2x+12-x^2-6x \\=-x^2-4x+12 \\=-(x-2)^2+16\)

Область определения: \(x \in \mathbb{R}\);

Область значений: \(y \in (-\infty, 16]\);

Функция убывает при \(x \in [-2, +\infty)\), функция возрастает при \(x \in (-\infty, -2]\);

Функция не является чётной или нечётной;

\(y > 0\) при \(x \in (-6, 2)\);

\(y < 0\) при \(x \in (-\infty, -6) \cup (2, +\infty)\).