Линия жизни
2016
Постройте график функции \(y=x^{2}-3\). Укажите промежутки, в которых функция принимает:
a) положительные значения;
б) отрицательные значения.
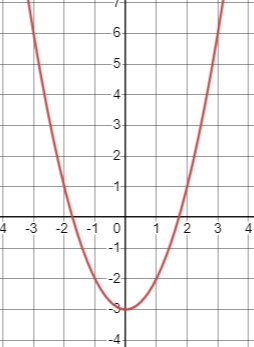
Для функции \(y = x^2 - 3\), найдем точки, где она обращается в ноль:
\(x^2 - 3 = 0\)
Это уравнение имеет два решения:
\(x^2 = 3\)
\(x = \pm \sqrt{3}\)
Таким образом, функция обращается в ноль при \(x = \sqrt{3}\) и \(x = -\sqrt{3}\). Теперь мы можем рассмотреть знак функции на интервалах между и за пределами этих точек.
•
Положительные значения:
На интервале \((- \infty, -\sqrt{3})\) и \((\sqrt{3}, + \infty)\) функция \(y = x^2 - 3\) принимает положительные значения, так как при \(x \sqrt{3}\) каждый квадрат \(x^2\) больше 3.
•
Отрицательные значения:
На интервале \((- \sqrt{3}, \sqrt{3})\) функция \(y = x^2 - 3\) принимает отрицательные значения, так как при \(-\sqrt{3} < x < \sqrt{3}\) каждый квадрат \(x^2\) меньше 3.
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Постройте график функции \(y=x^{2}-3\). Укажите промежутки, в которых функция принимает: a) положительные значения; б) отрицательные значения.
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
