§6. Неравенства с одной переменной — 16. Решение неравенств второй степени с одной переменной — 265 — стр. 91

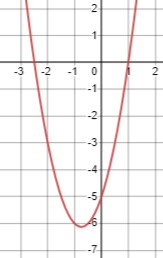
\(2x^2+3x-5 \geq 0\)

Решим уравнение \(2x^2+3x-5=0\):

\(x_{1,2} = \frac{-3 \pm \sqrt{3^2-4 \cdot 2 \cdot (-5)}}{4}\)

\(D = 49\)

\(x_{1,2} = \frac{-3 \pm \sqrt{49}}{4}\)

\(x_1 = \frac{-3 + 7}{4} = 1\)

\(x_2 = \frac{-3 - 7}{4} = -2.5\)

Теперь рассмотрим интервалы между найденными корнями и за пределами:

\(x \in (-\infty; -2.5) \cup (1; +\infty)\).

\(-6x^2+6x+36 \geq 0\)

Решим уравнение \(-6x^2+6x+36=0\):

\(-6x^2+6x+36=0 \\ x^2-x-6=0 \\ x_{1,2}=\frac{1 \pm \sqrt{1+24}}{2} \\ x_1=-2, \\ x_2=3\)

Теперь рассмотрим интервалы между найденными корнями и за пределами:

\(x \in (-2 ; 3)\).

\(-x^2+5 \leq 0\)

Решим уравнение \(-x^2+5=0\):

\(x_{1,2} = \pm \sqrt{5}\)

Рассмотрим интервалы между найденными корнями и за пределами:

\(x \in (-\infty ;-\sqrt{5}) \cup (\sqrt{5} ;+\infty)\).