§6. Неравенства с одной переменной — 16. Решение неравенств второй степени с одной переменной — 273 — стр. 91

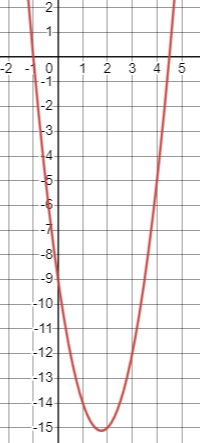
\(2 x(3 x-1)>4 x^{2}+5 x+9\)

Переносим все члены в левую часть:

\(6 x^{2}-2 x>4 x^{2}+5 x+9\)

Упростим выражение:

\(2 x^{2}-7 x-9>0\)

Уравнение \(2 x^{2}-7 x-9=0\) имеет корни:

\(x_{1,2}=\frac{7 \pm \sqrt{49+72}}{4}\)

\(x_{1}=-1\)

\(x_{2}=\frac{9}{2}\)

Таким образом, неравенство \(2 x(3 x-1)>4 x^{2}+5 x+9\) выполняется при \(x \in (-\infty, -1) \cup (\frac{9}{2}, +\infty)\).

Ответ: \(x \in (-\infty, -1) \cup (\frac{9}{2}, +\infty)\).

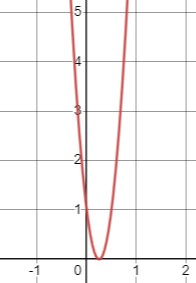
\((5 x+7)(x-2)<21 x^{2}-11 x-13\)

Переносим все члены в левую часть:

\(5 x^{2}-3 x-14>21 x^{2}-11 x-13\)

Упростим выражение:

\(16 x^{2}-8 x+1>0\)

Уравнение \(16 x^{2}-8 x+1=0\) имеет корень:

\(x=\frac{1}{4}\)

Так как \(16 x^{2}-8 x+1\) — это парабола с ветвями, направленными вверх, знак выражения зависит от интервалов между корнями. Таким образом, неравенство выполняется при \(x \in (-\infty, \frac{1}{4}) \cup (\frac{1}{4}, +\infty)\).

Ответ: \(x \in (-\infty, \frac{1}{4}) \cup (\frac{1}{4}, +\infty)\).