§6. Неравенства с одной переменной — 17. Решение неравенств методом интервалов — 297 — стр. 98

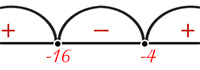
Рассмотрим неравенство \(\frac{x-8}{x+4} > 2\). Область допустимых значений: \(x \neq -4\). Умножим обе стороны на \((x+4)\) (поскольку \(x+4\) не может быть равным нулю): \((x-8) - 2(x+4) < 0\). Упростим: \(-x - 16 < 0\). Перейдем к равенству: \(\frac{x+16}{x+4} < 0\). Решим неравенство: \(x_{1} = -16\), \(x_{2} = -4\), \(x \in (-16, -4)\).

Рассмотрим неравенство \(\frac{3-x}{x-2} < 1\). Область допустимых значений: \(x \neq 2\). Умножим обе стороны на \((x-2)\) (поскольку \(x-2\) не может быть равным нулю): \((3-x) - (x-2) < 0\). Упростим: \(-2x + 5 < 0\). Перейдем к равенству: \(\frac{x-5}{x-2} > 0\). Решим неравенство: \(x_{1} = 2\), \(x_{2} = 2.5\), \(x \in (-\infty, 2) \cup (2.5, +\infty)\).

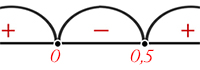
Рассмотрим неравенство \(\frac{7x-1}{x} > 5\). Область допустимых значений: \(x \neq 0\). Умножим обе стороны на \(x\) (поскольку \(x\) не может быть равным нулю): \((7x-1) - 5x > 0\). Упростим: \(-2x + 1 > 0\). Перейдем к равенству: \(\frac{x-1}{2} > 0\). Решим неравенство: \(x_{1} = 0.5\), \(x_{2} = 0\), \(x \in (-\infty, 0) \cup (0.5, +\infty)\).

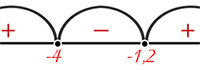
Рассмотрим неравенство \(\frac{6-2x}{x+4} > 3\). Область допустимых значений: \(x \neq -4\). Умножим обе стороны на \((x+4)\) (поскольку \(x+4\) не может быть равным нулю): \((6-2x) - 3(x+4) > 0\). Упростим: \(-5x - 6 > 0\). Перейдем к равенству: \(\frac{x+6}{5} > 0\). Решим неравенство: \(x_{1} = -1.2\), \(x_{2} = -4\), \(x \in (-4, -1.2)\).