Вертикаль
2016
(Для работы в парах.) Изобразите на координатной плоскости множество решений неравенства:
a) \(xy<4\); б) \(xy>-6\).
1) Разберите совместно пример 3, приведённый в пункте 23.
2) Распределите, кто выполняет задание а), а кто - задание б), и выполните их.
3) Проверьте друг у друга правильность выполнения задания и исправьте ошибки, если они допущены.
а
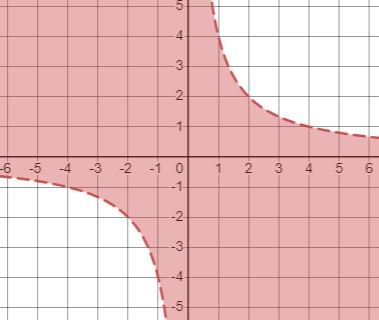
Неравенство \(xy<4\) означает, что произведение \(x\) и \(y\) должно быть меньше 4. Рассмотрим два случая:
1. Когда \(x > 0\): В этом случае, чтобы удовлетворять неравенству, \(y\) должно быть меньше 4.
2. Когда \(x < 0\): В этом случае, чтобы удовлетворять неравенству, \(y\) должно быть больше 4.
Также включим случай \(x=0, y=0\).
б
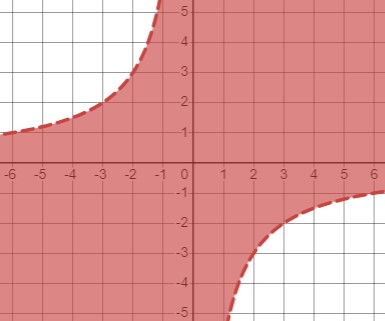
Неравенство \(xy>-6\) означает, что произведение \(x\) и \(y\) должно быть больше -6. Рассмотрим два случая:
1. Когда \(x > 0\): В этом случае, чтобы удовлетворять неравенству, \(y\) должно быть больше \(-\frac{6}{x}\).
2. Когда \(x < 0\): В этом случае, чтобы удовлетворять неравенству, \(y\) должно быть меньше \(-\frac{6}{x}\).
Также необходимо учесть, что \(x \neq 0\) и \(y \neq 0\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
(Для работы в парах.) Изобразите на координатной плоскости множество решений неравенства: a) \(xy<4\); б) \(xy>-6\). 1) Разберите совместно пример 3, приведённый в пункте 23. 2) Распределите, кто выполняет задание а), а кто - задание б), и выполните их. 3) Проверьте друг у друга правильность выполнения задания и исправьте ошибки, если они допущены.
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
