§8. Неравенства с двумя переменными и их системы — 24. Системы неравенств с двумя переменными — 466 — стр. 138

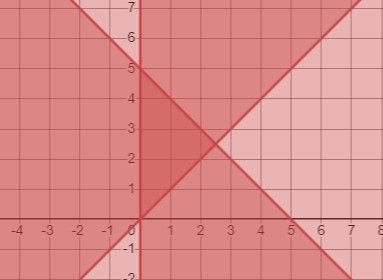
Рассмотрим систему неравенств:

\(\begin{cases} x-y \leq 0 \\ x+y \leq 5 \\ x \geq 0 \end{cases}\)

Преобразуем систему:

\(\begin{cases} y \geq x \\ y \leq 5-x \\ x \geq 0 \end{cases}\)

Множество решений системы неравенств задает треугольник. Найдем площадь треугольника, используя формулу \(S=\frac{1}{2} a h\), где \(a\) - длина основания, \(h\) - высота.

Вершина треугольника - точка пересечения прямых \(y=x\) и \(y=5-x: \\(x=5-x \\ x=2.5\), следовательно, \(y=2.5\).

Высота треугольника: \(h=2.5\).

Длина основания треугольника: \(a=5\).

\(S=\frac{1}{2} \cdot 2.5 \cdot 5 = 6.25 \, \text{ед}^2\).

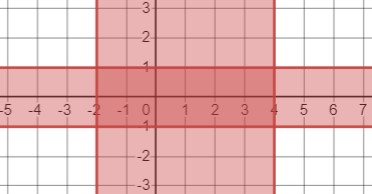
Рассмотрим систему неравенств:

\(\begin{cases} -2 \leq x \leq 4 \\ -1 \leq y \leq 1 \end{cases}\)

Множество решений системы неравенств задает прямоугольник. Найдем площадь прямоугольника, используя формулу \(S=a \cdot b\), где \(a\) - длинная сторона, \(b\) - короткая сторона.

Длинная сторона: \(a=4-(-2)=6\).

Короткая сторона: \(b=1-(-1)=2\).

\(S=2 \cdot 6 = 12 \, \text{ед}^2\).