§8. Неравенства с двумя переменными и их системы — Дополнительные упражнения к параграфу 7 — 484 — стр. 144

Уравнение, график которого представляет собой окружность: \(x^2 + y^2 - 2x - 4y + 5 = 0 \)

Приведя подобные, получаем:

\((x - 1)^2 + (y - 2)^2 = 0\), что описывает точку (1, 2).

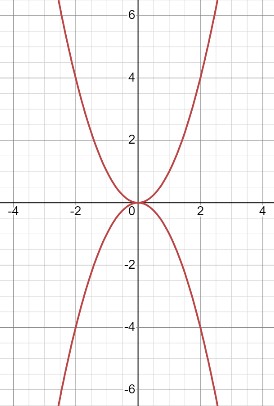
Уравнение, графиком которого являются две ветви параболы: \(y^2 - x^4 = 0 \)

Разложим на множители:

\((y - x^2)(y + x^2) = 0\), что дает уравнения двух ветвей:

\(y = x^2 \quad \text{и} \quad y = -x^2\).