Инновационная школа
2018
Изобразите на координатной плоскости множество точек, заданное неравенством:
a) \((x - 3)^{2} + (y + 3)^{2} \leq 4\);
б) \(y \leq x^{2} - 5x + 6\).
а
Неравенство \((x-3)^2 + (y+3)^2 \leq 4\) представляет собой множество точек, включая окружность с центром в точке \((3, -3)\) и радиусом 2.
б
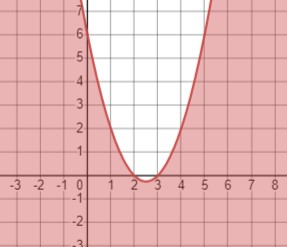
Неравенство \(y \leq x^2 - 5x + 6\) означает множество точек, расположенных ниже графика функции \(y = x^2 - 5x + 6\), включая сам график.
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Изобразите на координатной плоскости множество точек, заданное неравенством: a) \((x - 3)^{2} + (y + 3)^{2} \leq 4\); б) \(y \leq x^{2} - 5x + 6\).
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
