§8. Неравенства с двумя переменными и их системы — Дополнительные упражнения к параграфу 8 — 519 — стр. 148

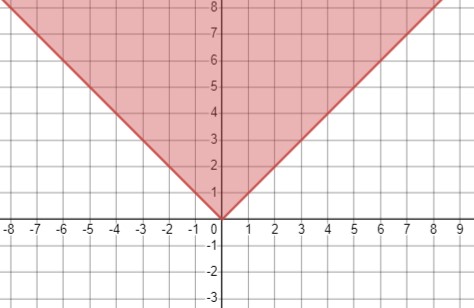
Неравенство \(y \geq |x|\) может быть записано как:

\(\begin{cases}y \geq x\\y \geq -x\end{cases}\)

Таким образом, множество точек, удовлетворяющих данному неравенству, включает в себя все точки, находящиеся выше графика функции \(y=|x|\), включая точки, принадлежащие графику.

Неравенство \(y \leq |x-2|\) может быть записано как:

\(2 - x \leq y \leq x - 2\)

Таким образом, множество точек, удовлетворяющих данному неравенству, находится ниже графика функции \(y=|x-2|\), включая точки, принадлежащие графику.