§9. Арифметическкая прогрессия — Дополнительные упражнения к параграфу 8 — 524 — стр. 151

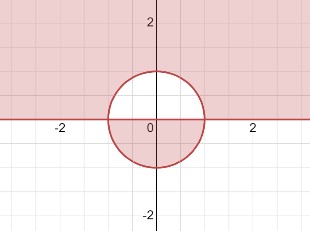
Рассмотрим неравенство \(y(x^2+y^2-1) \geq 0 \). Решение данного неравенства можно представить в виде системы:

\(\begin{cases}y \geq 0 \\x^2+y^2 \geq 1\end{cases}\) или \(\begin{cases}y \leq 0 \\x^2+y^2 \leq 1\end{cases}\)

Это можно упростить до

\(\begin{cases}y \geq 0 \\x^2+y^2 \geq 1\end{cases}\) или \(\begin{cases}y \leq 0 \\x^2+y^2 \leq 1\end{cases}\)

Где \(y=0 \) представляет собой прямую, а \(x^2+y^2=1 \) - окружность с центром в начале координат и радиусом 1.

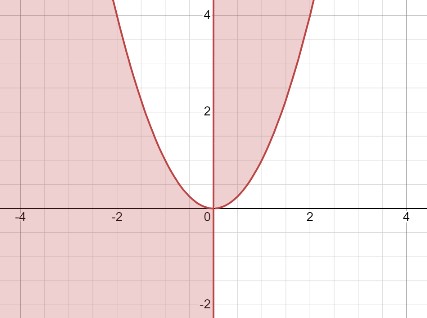
Теперь рассмотрим неравенство \(x(x^2-y) \leq 0 \). Его решение может быть представлено в виде системы:

\(\begin{cases}x \leq 0 \\x^2-y \geq 0\end{cases}\) или \(\begin{cases}x \geq 0 \\x^2-y \leq 0\end{cases}\)

Это можно упростить до

\(\begin{cases}x \leq 0 \\y \leq x^2\end{cases}\) или \(\begin{cases}x \geq 0 \\y \geq x^2\end{cases}\)

Где \(x=0 \) представляет собой вертикальную прямую, а \(y=x^2 \) - параболу.