Физика
2024
Не выполняя построения, выясните, пересекаются ли:
а) парабола \(y=x^{2}-6 x+8\) и прямая \(x+y=4\);
б) прямая \(x+y=4\) и гипербола \(y=\frac{3}{x}\);
в) окружности \(x^{2}+y^{2}=4\) и \((x-3)^{2}+y^{2}=1\);
г) окружность \((x-1)^{2}+(y-2)^{2}=4\) и прямая \(x+2 y=3\).
Если пересекаются, то укажите координаты точек пересечения. Проиллюстрируйте решение с помощью графиков.
а
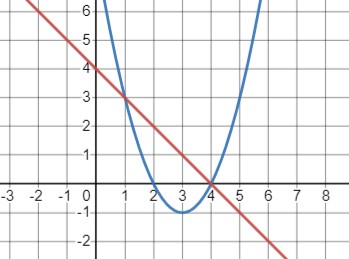
\(\begin{cases}y=x^2-6 x+8 \\ x+y=4\end{cases}\)
\(\begin{cases}y=4-x \\ x^2-6 x+8=4-x\end{cases}\)
\(\begin{cases}y=4-x \\ x^2-5 x+4=0\end{cases}\)
\(x^2-5 x+4=0, \\ x_{1,2}=\frac{5 \pm \sqrt{25-16}}{2}, \\ x_1=4, \\ x_2=1\)
\(\begin{cases}{ x = 4 } \\ { y = 0 }\end{cases} \text { или } \begin{cases}x=1 \\ y=3\end{cases}\)
Ответ: пересекаются в точках \((4 ; 0)\) и \((1 ; 3)\).
б
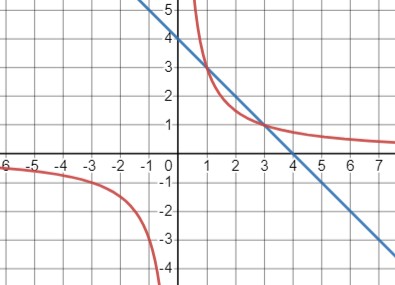
\(\begin{cases}x+y=4 \\ y=\frac{3}{x}\end{cases}\)
\(\begin{cases}y=\frac{3}{x} \\ x+\frac{3}{x}-4=0\end{cases}\)
\(\begin{cases}y=\frac{3}{x} \\ x^2-4 x+3=0\end{cases}\)
\(x^2-4 x+3=0 \\ x_{1,2}=\frac{4 \pm \sqrt{16-12}}{2} \\ x_1=3 \\ x_2=1\)
\(\begin{cases}{ x = 3 } \\ { y = 1 }\end{cases} \text { или }\begin{cases}x=1 \\ x=3\end{cases}\)
Ответ: пересекаются в точках \((3 ; 1)\) и \((1 ; 3)\).
в
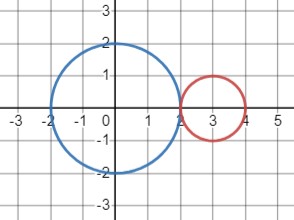
\(\begin{cases}x^2+y^2=4 \\ (x-3)^2+y^2=1\end{cases}\)
\(\begin{cases}y^2=4-x^2 \\ x^2-6 x+9+4-x^2-1=0\end{cases}\)
\(\begin{cases}y^2=4-x^2 \\ -6 x+12=0\end{cases}\)
\(\begin{cases}x=2 \\ y=0\end{cases}\)
Ответ: пересекаются в точке \((2 ; 0)\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Не выполняя построения, выясните, пересекаются ли: а) парабола \(y=x^{2}-6 x+8\) и прямая \(x+y=4\); б) прямая \(x+y=4\) и гипербола \(y=\frac{3}{x}\); в) окружности \(x^{2}+y^{2}=4\) и \((x-3)^{2}+y^{2}=1\); г) окружность \((x-1)^{2}+(y-2)^{2}=4\) и прямая \(x+2 y=3\). Если пересекаются, то укажите координаты точек пересечения. Проиллюстрируйте решение с помощью графиков.
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
