Вертикаль
2016
Изобразите множество точек, координаты которых удовлетворяют системе:
а) \(\left\{\begin{array}{l}x^2 + y^2 \leq 4, \\ |x| \geq 1;\end{array}\right.\)
б) \(\left\{\begin{array}{l}x^2 + y^2 \leq 9, \\ |y| \geq 2.\end{array}\right.\)
а
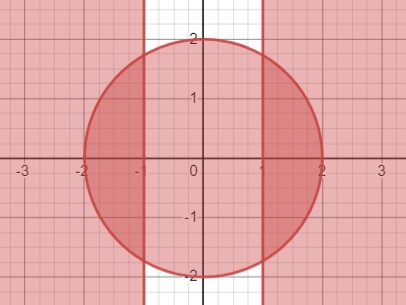
\(\begin{cases}x^2+y^2 \leq 4 \\ |x| \geq 1\end{cases}\)
\(\begin{cases}x^2+y^2 \leq 4 \\ x \leq-1, x \geq 1\end{cases}\)
\(x^2+y^2=4\) - окружность с центром в начале координат и радиусом 2.
\(x=1\) - прямая справа
\(x=-1\) - прямая слева.
б
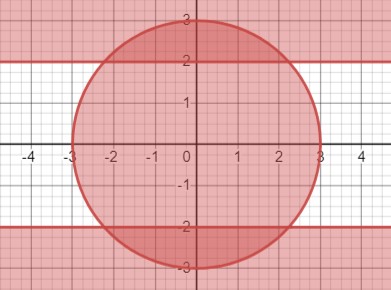
\(\begin{cases}x^2+y^2 \leq 9 \\ |y| \geq 2\end{cases}\)
\(\begin{cases}x^2+y^2 \leq 9 \\ y \leq-2, y \geq 2\end{cases}\)
\(x^2+y^2=9\) - окружность с центром в начале координат и радиусом 3.
\(y=2\) - прямая сверху
\(y=-2\) - прямая снизу.
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Изобразите множество точек, координаты которых удовлетворяют системе: а) \(\left\{\begin{array}{l}x^2 + y^2 \leq 4, \\ |x| \geq 1;\end{array}\right.\) б) \(\left\{\begin{array}{l}x^2 + y^2 \leq 9, \\ |y| \geq 2.\end{array}\right.\)
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
