Обществознание
2017
(Для работы в парах.) Постройте график функции:
a) \(y=\frac{x^{2}-25}{2 x+10}\);
б) \(y=\frac{x^{3}-9 x}{x^{2}-9}\).
1) Обсудите, что общего у дробей, задающих функцию в заданиях а) и б). Как надо учитывать эту особенность при построении графиков?
2) Распределите, кто выполняет задание а), а кто - задание б), и выполните их.
3) Проверьте друг у друга, правильно ли выполнено задание. Исправьте замеченные ошибки.
а
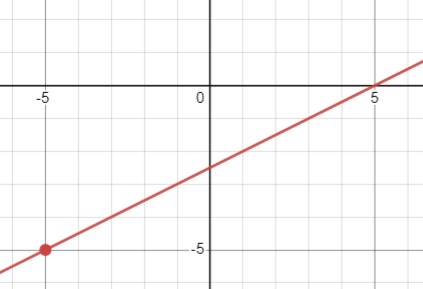
\(y=\frac{x^{2}-25}{2 x+10}\)
Условие \(2x + 10 \neq 0\) говорит о том, что знаменатель не должен быть равен нулю, и это соответствует условию \(x \neq -5\). Таким образом, область определения функции - \(x \in (-\infty, -5) \cup (-5, +\infty)\).
Далее, мы сокращаем дробь \(\frac{x^2 - 25}{2x + 10}\) до \(\frac{(x - 5)(x + 5)}{2(x + 5)}\) и упрощаем до \(\frac{x - 5}{2}\). Это эквивалентно уравнению \(y = \frac{x - 5}{2}\). График этой функции - прямая линия.
б
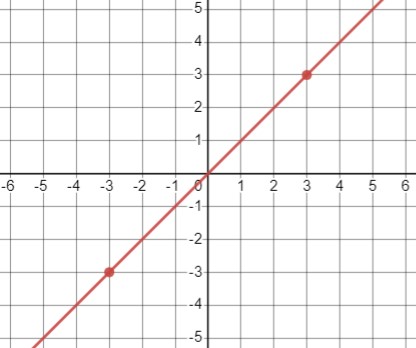
\(y=\frac{x^{3}-9 x}{x^{2}-9}\)
Условие \(x^2 - 9 \neq 0\) означает, что знаменатель не должен быть равен нулю, что соответствует условиям \(x \neq 3\) и \(x \neq -3\). Таким образом, область определения функции - \(x \in (-\infty, -3) \cup (-3, 3) \cup (3, +\infty)\).
Мы сокращаем дробь \(\frac{x^3 - 9x}{x^2 - 9}=\frac{x(x^2 - 9}{x^2 - 9}=x\). Это эквивалентно уравнению \(y = x\). График этой функции - также прямая линия.
Таким образом, для обеих функций графики представляют собой прямые линии, и их области определения учитывают ограничения, связанные с знаменателем.
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
(Для работы в парах.) Постройте график функции: a) \(y=\frac{x^{2}-25}{2 x+10}\); б) \(y=\frac{x^{3}-9 x}{x^{2}-9}\). 1) Обсудите, что общего у дробей, задающих функцию в заданиях а) и б). Как надо учитывать эту особенность при построении графиков? 2) Распределите, кто выполняет задание а), а кто - задание б), и выполните их. 3) Проверьте друг у друга, правильно ли выполнено задание. Исправьте замеченные ошибки.
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
