Прямоугольный параллелепипед со сторонами основания \(a\) см и \(b\) см и высотой \(20\) см имеет объём, равный \(120 \mathrm{cм}^{3}\). Выразите формулой зависимость \(b\) от \(a\). Является ли эта зависимость обратной пропорциональностью? Какова область определения этой функции? Постройте график.
У нас есть формула для объема параллелепипеда: \( V = a b h \), где \( a \), \( b \), и \( h \) - длины сторон параллелепипеда.
Из условия задачи нам известно, что объем \( V \) равен 120, а высота \( h \) равна 20 единицам. Таким образом, у нас имеется уравнение \( 120 = a b \cdot 20 \).
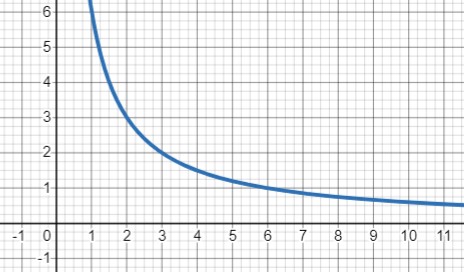
Далее, мы выражаем одну из переменных через другую, чтобы получить зависимость между ними. В данном случае, мы выражаем \( b \) через \( a \), получая \( b = \frac{120}{20a} = \frac{6}{a} \).
Таким образом, мы получаем зависимость, которая является обратной пропорциональностью между длиной \( b \) и длиной \( a \). Областью определения является \( a > 0 \), что вполне логично, так как длины сторон должны быть положительными числами.
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Прямоугольный параллелепипед со сторонами основания \(a\) см и \(b\) см и высотой \(20\) см имеет объём, равный \(120 \mathrm{cм}^{3}\). Выразите формулой зависимость \(b\) от \(a\). Является ли эта зависимость обратной пропорциональностью? Какова область определения этой функции? Постройте график.

