Выясните, при каких целых \(a\) дробь \(\frac{a^{2}-4 a+1}{a-2}\) принимает целые значения, и найдите эти значения.
Мы начинаем с выделения полного квадрата в числителе дроби:
\(\frac{a^2 - 4a + 1}{a - 2} = \frac{(a^2 - 4a + 4) - 3}{a - 2} = \frac{(a - 2)^2 - 3}{a - 2} = a - 2 - \frac{3}{a - 2}\)
Дробь \(\frac{3}{a - 2}\) будет целой при \(a - 2 = \{-3, -1, 1, 3\}\), то есть при \(a = \{-1, 1, 3, 5\}\).
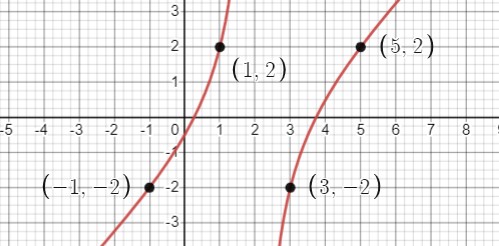
\(\begin{array}{|c|c|}\hline a & \frac{a^2 - 4a + 1}{a - 2}=a - 2 - \frac{3}{a - 2} \\\hline-1 & -2 \\1 & 2 \\3 & -2 \\5 & 2 \\\hline\end{array}\)
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Выясните, при каких целых \(a\) дробь \(\frac{a^{2}-4 a+1}{a-2}\) принимает целые значения, и найдите эти значения.

