Вертикаль.
2015
Постройте график функции:
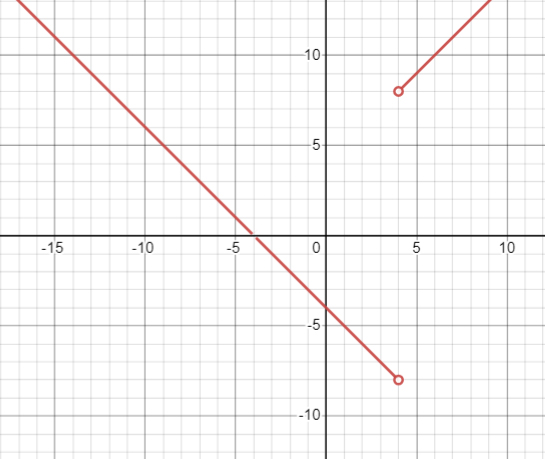
а) \(y=\frac{x^{2}-16}{|x-4|}\)
б) \(y=\frac{x^{2}-25}{5+|x|}\).
а
\(y=\frac{x^{2}-16}{|x-4|}=\frac{(x-4)(x+4)}{|x-4|}=\begin{cases}-x-4, \quad x4\end{cases}, \quad x \neq 4\)
б
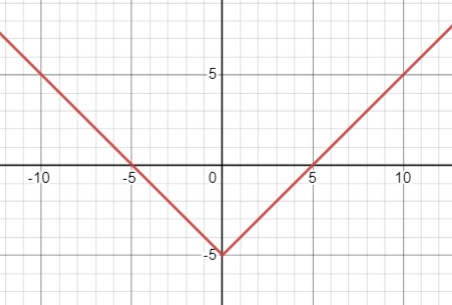
\(y=\frac{x^{2}-25}{5+|x|}=\begin{cases}\frac{(x-5)(x+5)}{5-x}, \quad x<0 \\\frac{(x-5)(x+5)}{5+x}, \quad x \geq 0\end{cases} \)
\(y=\begin{cases}-x-5, \quad x<0 \\x-5, \quad x \geq 0\end{cases}\)
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Постройте график функции: а) \(y=\frac{x^{2}-16}{|x-4|}\) б) \(y=\frac{x^{2}-25}{5+|x|}\).
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
