Дополнительные упражнения к главе I — К параграфу 3 — 267 — стр. 63

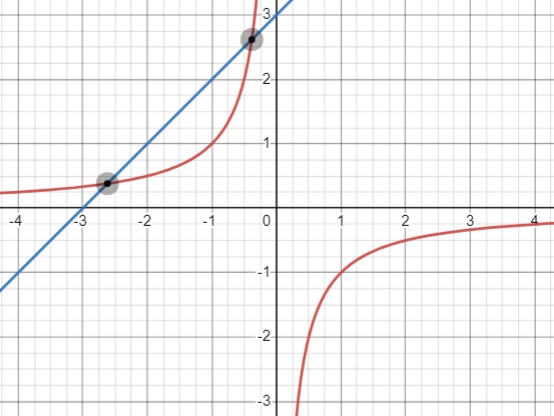
Условие пересечения гиперболы и прямой в двух точках: \(b^2+a k>0\).

Анализ корней:

- Если оба корня находятся в одной четверти, то они одного знака (\(x_1 x_2 > 0\)).

- Это означает, что \(-\frac{k}{a}>0\) и следовательно \(\frac{k}{a}<0\), то есть \(k\) и \(a\) имеют разные знаки.

- Величина \(|b|\) ограничена снизу:

\(\begin{cases}a k<0\\b^2>-a k \end{cases}\).

Невозможность пересечения:

- Гипербола не может находиться в первой и второй четвертях, поэтому такое пересечение невозможно.

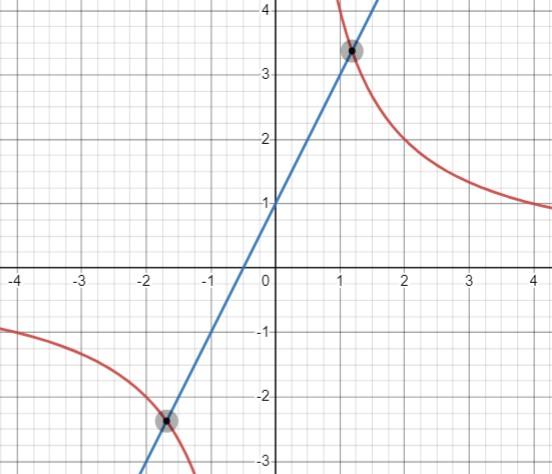
Пересечение в первой и третьей четвертях:

- Корни разного знака (\(x_1 x_2 < 0\)).

- Это означает, что \(-\frac{k}{a} < 0\), и следовательно \(\frac{k}{a}>0\), то есть \(k\) и \(a\) имеют одинаковые знаки.

- Поскольку гипербола и прямая проходят через первую и третью четверть, этот знак положительный.

- В этом случае \(b^2>-a k\) означает, что \(b\) может быть любым:

\(\begin{cases}k>0 \\a>0 \\b \in \mathbb{R}\end{cases} \).