При каких значениях \(a\) и \(b\) графики функций \(y=x+b\) и \(y=a x-2 b\) пересекаются в точке \((3 ; 1)\)?
Система уравнений: Подставляя известные значения \(x\) и \(y\), мы получаем систему уравнений, чтобы определить значения \(a\) и \(b\):
\(\begin{cases}1 = 3 + b \\1 = 3a - 2b\end{cases}\)
Решение системы уравнений: Решив систему, мы находим, что \(b = -2\) и \(a = \frac{1 + 2b}{3} = -1\).
Прямые: Мы определяем уравнения прямых: \(y = x - 2\) и \(y = -x + 4\). Это происходит после определения коэффициентов \(a\) и \(b\).
График: Построен график прямых \(y = x - 2\) и \(y = -x + 4\), который отображен на рисунке.
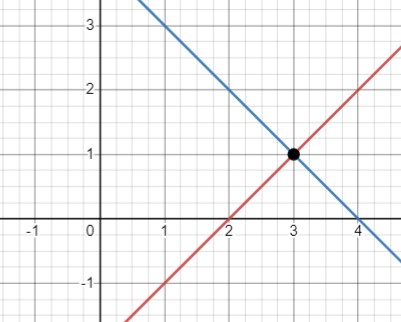
Таким образом, мы получаем систему прямых, как описано выше, что подтверждается графически.
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
При каких значениях \(a\) и \(b\) графики функций \(y=x+b\) и \(y=a x-2 b\) пересекаются в точке \((3 ; 1)\)?

