(Для работы в парах.) Имеют ли общие точки графики функций:
а) \(y=\sqrt{x}\) и \(y=x\);
б) \(y=\sqrt{x}\) и \(y=1000\);
в) \(y=\sqrt{x}\) и \(y=x+10\);
г) \(y=\sqrt{x}\) и \(y=-x+1,5\)?
При положительном ответе укажите координаты этих точек.
1) Распределите, кто выполняет задания а) и в), а кто - задания б) и г), и выполните их.
2) Проверьте друг у друга, верно ли выполнены задания. Исправьте замеченные ошибки.
3) Приведите примеры линейных функций, графики которых: не пересекают график функции \(y=\sqrt{x}\); пересекают его в одной точке; пересекают его в двух точках. Обсудите правильность этих примеров.
а
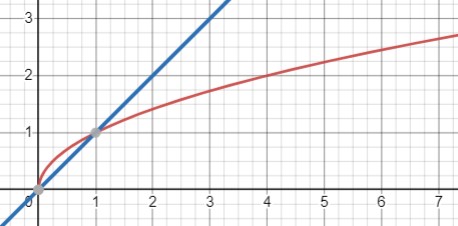
\(\sqrt{x}=x^2\)
\(x=x^2 \)
\(x^2-x=0 \)
\(x(x-1)=0\)
Отсюда получаем два корня: \(x=\{0; 1\}\).
Общие точки: \( (0, 0), (0, 1)\).
б
Графики для \(y=\sqrt{x}\) и \(y=1000\).
\(\sqrt{x}=1000\)
Один корень: \(x=1000000\)
Одна общая точка: \((100000 ; 1000)\).
в
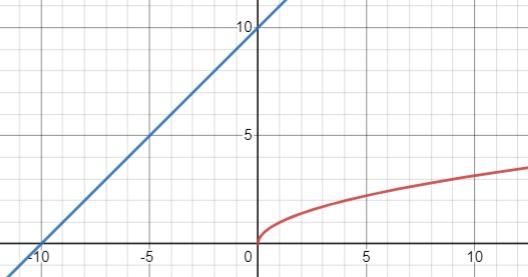
\(\sqrt{x}=x+10\)
\(\sqrt{x}=x+10 \)
\(x= (x+10)^2\)
\(x=x^2+20x+100\)
\(x^2+19x+100=0\)
Заметно, что уравнение \(x^2+19x+100=0\) не имеет действительных корней, т.к. дискриминант меньше нуля.
\(x=\emptyset\).
г
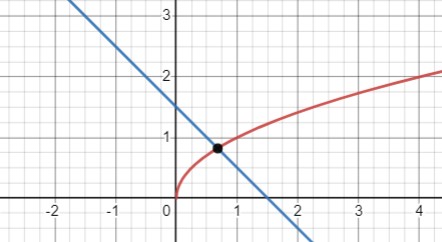
Графики для \(y=\sqrt{x}\) и \(y=-x+1,5\)
\(\sqrt{x}=-x+1,5\)
\(x=(-x+1,5)^2=(1,5-x)^2=(x-1,5)^2\)
\(x=x^2-3 x+2,25\)
\(x^2-4 x+2,25=0\)
\(D=4^2-4 \cdot 2,25=7>0\)
\(x=\frac{4 \pm \sqrt{7}}{2}=2 \pm \frac{\sqrt{7}}{2}\)
Два положительных корня.
\(y=-x+1,5=-2 \mp \frac{\sqrt{7}}{2}+1,5=-0,5 \mp \frac{\sqrt{7}}{2}\)
Положительный только один y.
Одна общая точка: \((2 - \frac{\sqrt{7}}{2}; -0,5+ \frac{\sqrt{7}}{2})\).
Нет точек пересечения: графики \(y=\sqrt{x}\) и \(y=x+1,5\)
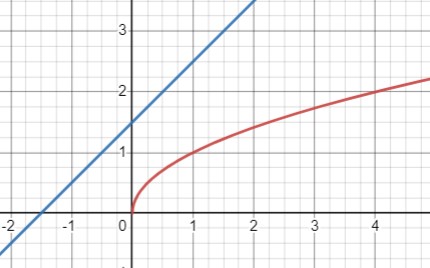
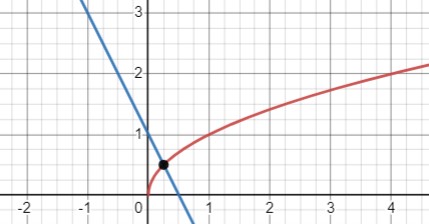
Одна точка пересечения: графики \(y=\sqrt{x}\) и \(y=-x+1\)
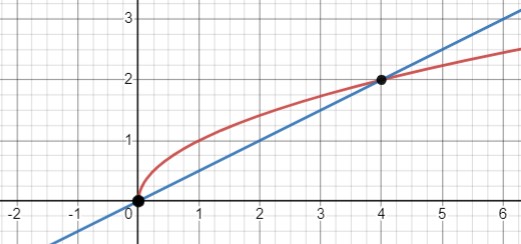
Две точки пересечения: графики \(y=\sqrt{x}\) и \(y=0,5x\)
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
(Для работы в парах.) Имеют ли общие точки графики функций: а) \(y=\sqrt{x}\) и \(y=x\); б) \(y=\sqrt{x}\) и \(y=1000\); в) \(y=\sqrt{x}\) и \(y=x+10\); г) \(y=\sqrt{x}\) и \(y=-x+1,5\)? При положительном ответе укажите координаты этих точек. 1) Распределите, кто выполняет задания а) и в), а кто - задания б) и г), и выполните их. 2) Проверьте друг у друга, верно ли выполнены задания. Исправьте замеченные ошибки. 3) Приведите примеры линейных функций, графики которых: не пересекают график функции \(y=\sqrt{x}\); пересекают его в одной точке; пересекают его в двух точках. Обсудите правильность этих примеров.
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
