С помощью графиков выясните, сколько корней может иметь при различных значениях \(b\) уравнение:
а) \(\sqrt{x}=x+b\);
б) \(\sqrt{x}=-x+b\).
Рассмотрим уравнение \(\sqrt{x}=x+b\).
Преобразуем его:
\(\sqrt{x}=x+b \\x-\sqrt{x}+b=0 \\(\sqrt{x})^2-\sqrt{x}+b=0\)
Вычислим дискриминант:
\(D=1-4 b \geq 0\)
Чтобы уравнение имело корни, необходимо, чтобы \(b\) удовлетворяло условию \(b \leq \frac{1}{4}\).
Значения \(\sqrt{x}\) определяются как:
\(\sqrt{x}=\frac{1 \pm \sqrt{1-4 b}}{2} \geq 0\)
Если \(b>\frac{1}{4}\), корней нет. При \(b=\frac{1}{4}\) получаем один корень \(\sqrt{x}=\frac{1}{2} \Rightarrow x=\frac{1}{4}\). При \(0 \leq b<\frac{1}{4}\) получаем два корня \(\sqrt{x}=\frac{1 \pm \sqrt{1-4 b}}{2} \Rightarrow x=\frac{(1 \pm \sqrt{1-4 b})^2}{4}\). При \(b<0\) получаем один корень \(\sqrt{x}=\frac{1+\sqrt{1-4 b}}{2} \Rightarrow x=\frac{(1+\sqrt{1-4 b})^2}{4}\).
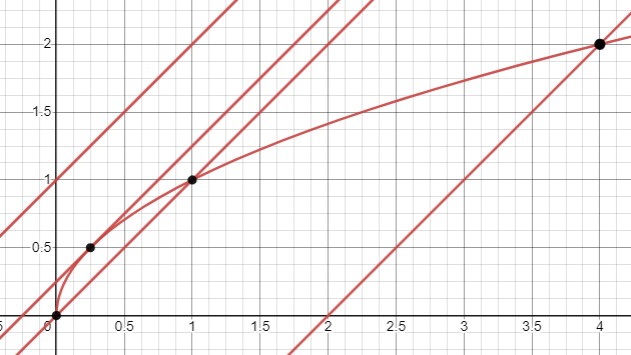
Теперь рассмотрим уравнение \(\sqrt{x}=-x+b\).
Преобразуем его:
\(\sqrt{x}=-x+b \\x+\sqrt{x}-b=0 \\(\sqrt{x})^2+\sqrt{x}-b=0\)
Вычислим дискриминант:
\(D=1+4 b \geq 0\)
Чтобы уравнение имело корни, необходимо, чтобы \(b\) удовлетворяло условию \(b \geq-\frac{1}{4}\).
Значения \(\sqrt{x}\) определяются как:
\(\sqrt{x}=\frac{-1 \pm \sqrt{1+4 b}}{2} \geq 0\)
Поскольку \(-1-\sqrt{1+4 b}<0\) для всех \(b\), остается только:
\(\sqrt{x}=\frac{-1+\sqrt{1+4 b}}{2} \geq 0\)
Требование \(-1+\sqrt{1+4 b} \geq 0\) дает \(b \geq 0\).
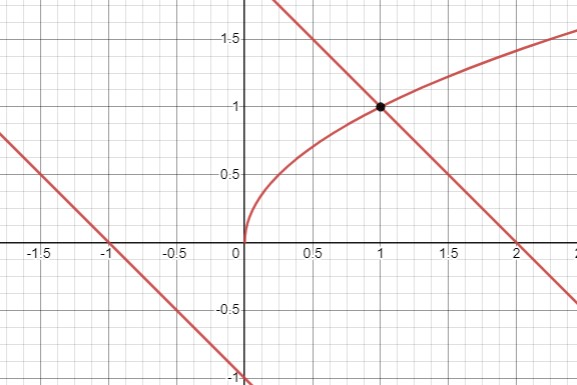
Если \(b<0\), корней нет. При \(b \geq 0\) получаем один корень \(x=\frac{(\sqrt{1+4 b}-1)^2}{4}\).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
С помощью графиков выясните, сколько корней может иметь при различных значениях \(b\) уравнение: а) \(\sqrt{x}=x+b\); б) \(\sqrt{x}=-x+b\).

