§ 9. Дробные рациональные уравнения — 26. Решение дробных рациональных уравнений — 642 — стр. 150

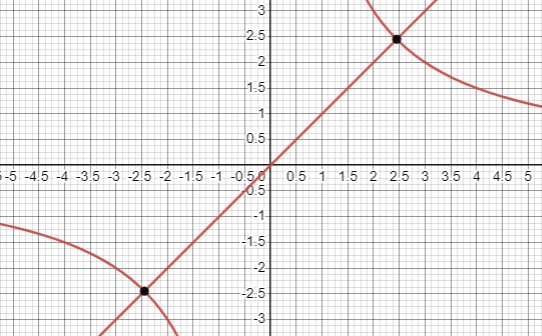
В данном уравнении $\frac{6}{x}=x$ мы начинаем с выявления корней. Мы находим два приблизительных значения для $x$, которые равны приблизительно $x\approx \pm 2,45$. Аналитически решая уравнение, мы приходим к квадратному уравнению $x^2=6$, откуда получаем корни $x_{1,2}=\pm \sqrt{6}$.

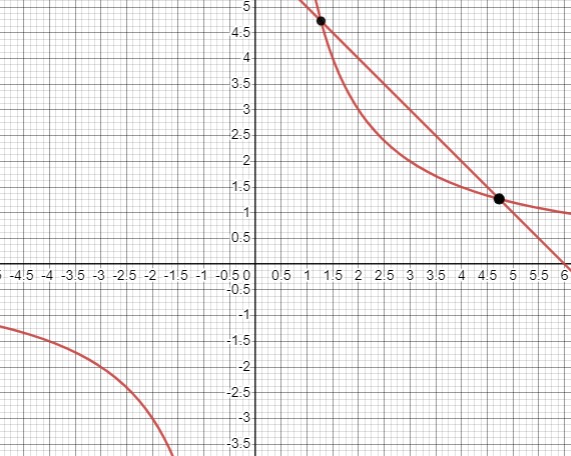
В уравнении $\frac{6}{x}=-x+6$ мы также выявляем два корня, которые приблизительно равны $x_1\approx 1,27$ и $x_2\approx 4,73$. Аналитически мы приходим к квадратному уравнению $x^2-6x+6=0$, для которого находим дискриминант $D=3^2-6=3$, и корни $x_{1,2}=3\pm \sqrt{3}$.