§ 10. Уравнения с двумя переменными и их системы — 30. Графический способ решения систем уравнений — 699 — стр. 164

Система уравнений:
\(\begin{cases}x^2 - 4 = 0 \\y^2 - 9 = 0\end{cases}\) приводит к следующим уравнениям: \(\begin{cases}|x| = 2 \\|y| = 3\end{cases}\)
Из уравнения \(x^2 - 4 = 0\) мы получаем \(|x| = 2\), что означает, что \(x\) может быть \(-2\) или \(2\). Аналогично, из уравнения \(y^2 - 9 = 0\) получаем \(|y| = 3\), что означает, что \(y\) может быть \(-3\) или \(3\).

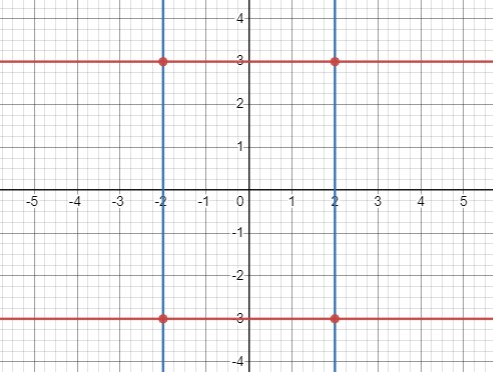
Итак, у нас четыре комбинации значений для \(x\) и \(y\):
\(\{(-2, -3), (-2, 3), (2, -3), (2, 3)\}\)
Каждая из этих четырех точек является решением системы уравнений.