Среди данных уравнений найдите уравнения параболы, гиперболы, прямой:
а) \(x y=-3\);
б) \(6 y-2=0\);
в) \(\frac{1}{4} y-x^{2}=-1\);
г) \(10+5 x y=0\);
д) \(1+2 x=0\);
e) \(2 x-2 y=5\).
Постройте график каждого уравнения.
Уравнение \(xy = -3\Rightarrow -\frac{3}{x}\) задает гиперболу, так как произведение \(xy\) постоянно. Функция \(y = -\frac{3}{x}\) демонстрирует, что гипербола находится во второй и четвертой четвертях плоскости.
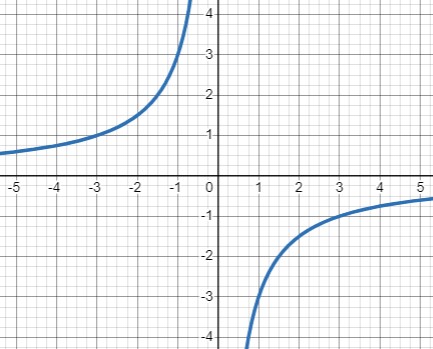
Уравнение \(6y - 2 = 0\Rightarrow y=\frac{1}{3}\) задает горизонтальную прямую. Она проходит через точку \((0, \frac{1}{3})\).
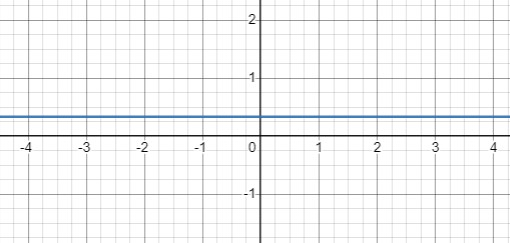
Уравнение \(\frac{1}{4}y - x^2 = -1 \Rightarrow y=4x^2-4\) определяет параболу с вершиной в точке \((0, -4)\), и ее ветви направлены вверх.
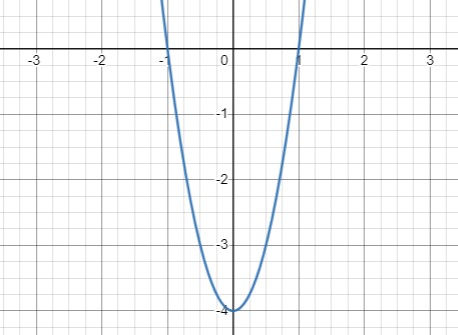
Уравнение \(10 + 5xy = 0 \Rightarrow xy=-2 \Rightarrow y=-\frac{2}{x}\) также определяет гиперболу. Его график находится во второй и четвертой четвертях, как и в случае уравнения (а).
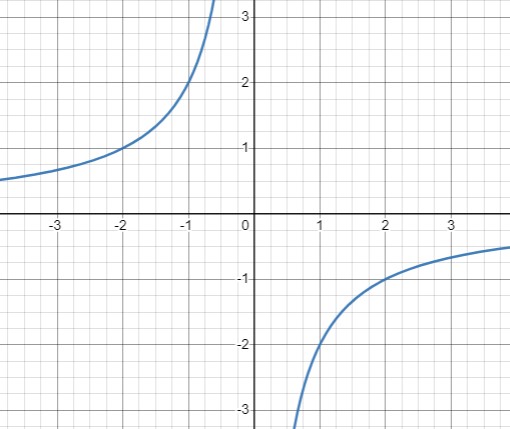
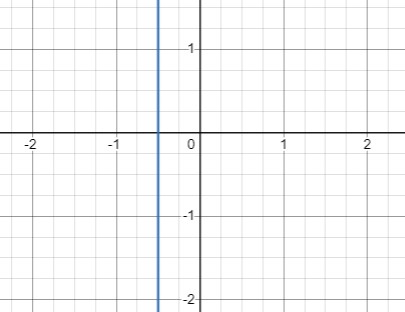
Уравнение \(1 + 2x = 0\Rightarrow x= -\frac{1}{2}\) задает вертикальную прямую, которая проходит через точку \((-0.5, 0)\).
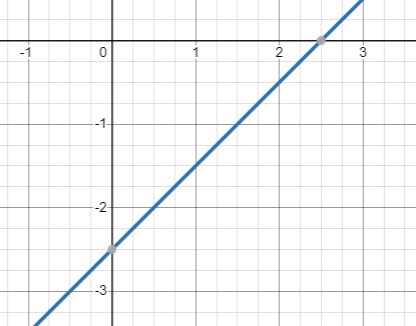
Уравнение \(2x - 2y = 5\Rightarrow y=x-2.5\) определяет прямую линию, проходящую через точку \((0, -2.5)\) с угловым коэффициентом \(k = 1\) и \(b=-2.5\).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Среди данных уравнений найдите уравнения параболы, гиперболы, прямой: а) \(x y=-3\); б) \(6 y-2=0\); в) \(\frac{1}{4} y-x^{2}=-1\); г) \(10+5 x y=0\); д) \(1+2 x=0\); e) \(2 x-2 y=5\). Постройте график каждого уравнения.

