История России.
2017
(Задача-исследование.) Сравните сумму длин медиан треугольника с его периметром.
1) Начертите произвольный треугольник \(A B C\) и проведите медиану \(B O\).
2) На луче \(B O\) отложите отрезок \(O D=B O\) и соедините точку \(D\) с точками \(A\) и \(C\). Какой вид имеет четырёхугольник \(A B C D\)? 3) Рассмотрите треугольник \(A B D\). Сравните \(2 m_{b}\) с суммой \(B C+A B\) ( \(m_{b}-\) медиана \(B O\) ).
4) Составьте аналогичные неравенства для \(2 m_{a}\) и \(2 m_{c}\).
5) Используя сложение неравенств, оцените сумму медиан треугольника \(m_{a}+m_{b}+m_{c}\).
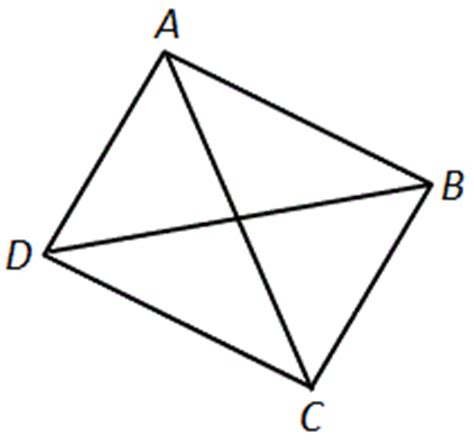
Данная задача рассматривает треугольник \(ABC\) с медианой \(BO\), где \(AO = OC\). Давайте подробнее рассмотрим шаги решения:
Из условия известно, что \(OD = BO\), следовательно, \(AO\) является медианой треугольника \(ABD\), так как \(ABCD\) - параллелограмм.
Согласно неравенству треугольника для треугольника \(ABC\):
\(AB + BC > AC\)
\(AB < AO + OB\)
\(BC < BO + OC\)
Далее, мы получаем:
\(AB + BC < AO + OB + OB + OC\)
\(AB + BC < 2OB + AO + OC\)
\(AB + BC < 2OB + AC\)
\(AB + BC - AC < 2OB\)
\(AB + BC - AC < 2m_b\)
\(m_b > \frac{AB + BC - AC}{2}\)
Аналогично для треугольника \(BCD\):
\(BC + CD > BD\)
\(BC + CD < BO + OC + OC + OD\)
\(BC + CD < 2OC + BD\)
\(BC + CD - BD < 2OC\)
\(BC + CD - BD < 2m_c\)
\(m_c > \frac{BC + CD - BD}{2}\)
Для треугольника \(ABD\):
\(AB + AD > BD\)
\(AB + AD < AO + BO + AO + OD\)
\(AB + AD < 2AO + BD\)
\(AB + AD - BD < 2AO\)
\(AB + AD - BD < 2m_a\)
\(m_a > \frac{AB + AD - BD}{2}\)
В итоге:
\(m_a + m_b + m_c > \frac{AB + AD - BD}{2} + \frac{AB + BC - AC}{2} + \frac{BC + CD - BD}{2}\)
\(m_a + m_b + m_c > \frac{AB + AD - BD + AB + BC - AC + BC + CD - BD}{2}\)
\(m_a + m_b + m_c > \frac{(AB + AD + BC + CD) + (-BD + AB - AC + BC - BD)}{2}\)
\(m_a + m_b + m_c > \frac{P}{2} + \frac{-BD + AB - AC + BC - BD}{2}\)
\( \frac{P}{2}< m_a + m_b + m_c< P\)
Вывод: Исходя из данной цепочки неравенств и равенств, мы получаем интересные результаты, которые могут быть полезны при решении подобных задач.
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
(Задача-исследование.) Сравните сумму длин медиан треугольника с его периметром. 1) Начертите произвольный треугольник \(A B C\) и проведите медиану \(B O\). 2) На луче \(B O\) отложите отрезок \(O D=B O\) и соедините точку \(D\) с точками \(A\) и \(C\). Какой вид имеет четырёхугольник \(A B C D\)? 3) Рассмотрите треугольник \(A B D\). Сравните \(2 m_{b}\) с суммой \(B C+A B\) ( \(m_{b}-\) медиана \(B O\) ). 4) Составьте аналогичные неравенства для \(2 m_{a}\) и \(2 m_{c}\). 5) Используя сложение неравенств, оцените сумму медиан треугольника \(m_{a}+m_{b}+m_{c}\).
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
