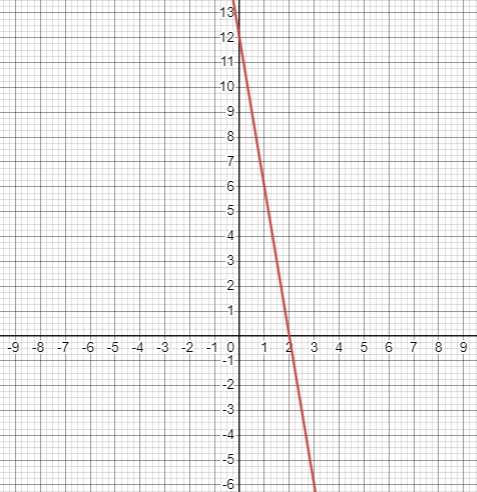
Найдите промежутки, в которых функция \(y=-6 x+12\) принимает положительные значения; отрицательные значения. Ответ проиллюстрируйте на графике.
Исходное уравнение представлено как \(y = -6x + 12\).
1. Рассмотрим неравенство \(-6x + 12 > 0\). Решим его:
\( -6x + 12 > 0\)
\(-6x > -12\)
\(x < 2.\)
Таким образом, при \(x < 2\), неравенство \(-6x + 12\) принимает положительные значения.
2. Теперь рассмотрим неравенство \(-6x + 12 < 0\). Решим его:
\(-6x + 12 < 0\)
\(-6x < -12 \)
\(x > 2\)
При \(x > 2\), выражение \(-6x + 12\) принимает отрицательные значения.
Из этого следует, что при \(x < 2\) функция \(y = -6x + 12\) принимает положительные значения, а при \(x > 2\) принимает отрицательные значения.
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Найдите промежутки, в которых функция \(y=-6 x+12\) принимает положительные значения; отрицательные значения. Ответ проиллюстрируйте на графике.

